BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm các chữ số đầu tiên của một số cực lớn có dạng $a^n \ (a, n \in \mathbb{N})$
- 05/02/2024
- 537 lượt xem
| Giả sử ta muốn tìm 3 chữ số đầu tiên của số $2023^{2024}$. |
Đặt $A=2023^{2024}$. Số các chữ số của $A$ là $[\log A]+1=[2024\log2023]+1$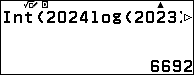 
Muốn tìm 3 chữ số đầu tiên của số $A$ ta lấy phần nguyên của số $\dfrac{A}{10^{6692-3}}$ bằng $\left[\dfrac{A}{10^{6692-3}}\right]=\left[\dfrac{10^{\log A}}{10^{6689}}\right]=\left[10^{2024\log 2023-6689}\right]$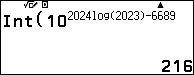 
 |
Chia sẻ
About TS. Nguyễn Thái Sơn
