BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Phương pháp CALC1000 tính $y$ theo $x$ từ phương trình $f(x,y)=0$
- 29/03/2024
- 212 lượt xem
| Trong các câu vận dụng cao của bài thi Tốt nghiệp THPT cho ta một biểu thức $f(x,y)=0$. Bài toán yêu cầu chúng ta xác định cụ thể $x$ và $y$ để một biểu thức $g(x,y)$ nào đó là lớn nhất hay nhỏ nhất. |
Đề thi MH 2024:
 |
Đề thi năm 2017
 |
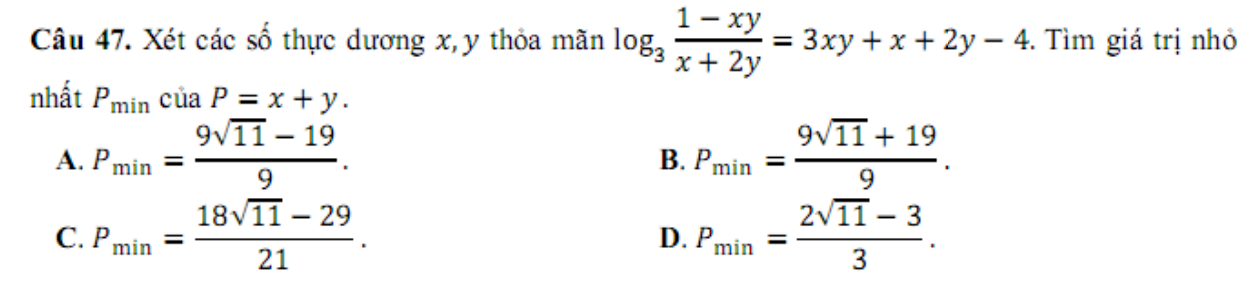Và hai bài tập tham khảo
1. Chuyên Vinh năm 2020
 |
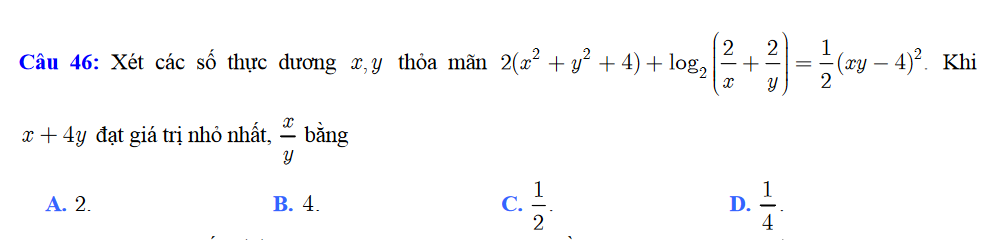2. Chuyên Lam Sơn (Thanh Hoá) năm 2020
 |
Trong bài này chúng ta sẽ giải bài thi minh hoạ 2024, các bài còn lại sẽ lần lượt xét trong các bài sau.
| Phương trình $f(x,y)=y\log_3(3x+y+9)-(x^2+3x+y)\log_3(x+3)=0$ phức tạp nên ta sẽ lưu nó vào biến nhớ f(x) để có thể sử dụng nhiều lần. Nhiệm vụ của chúng ta là Tính $y$ theo $x$ bằng cách cho $x=1000$ để tính $y$.
Khi lưu vào f(x) và giải phương trình tìm $y$ thì ta sẽ hoán vị vai trò của chữ $x$ và chữ $y$ vì lúc đó máy tính sẽ hiểu $f(x,y)=0$ là phương trình f(x) = 0 theo biến x. Sau đây là lời giải trên máy tính Casio fx-880BTG: |
- 1. Lưu biểu thức đã cho vào f(x) bằng cách hoán đổi vai trò của chữ $x$ và chữ $y$:
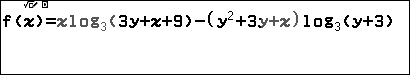
- 2.Cho $y=1000$ (tức là cho cho $x=1000$ trong phương trình gốc). Solver tìm $x$ (tức là tìm $y$ trong phương trình gốc)
Kết quả này cho ta $y=x^2+3x$. Khi đó $y-5x=x^2-2x$ với $x\geqslant 0$
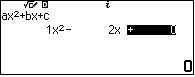
GIÁ TRỊ NHỎ NHẤT của nó đạt tại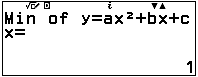
suy ra $y=4$. Vậy $x-2y=-7$ , chọn C.
- 1. Biểu thức $y=x^2+3x$ đã đúng với $x=1000$ theo phương pháp CALC1000. Trên Casio fx-880BTG ta vẫn có thể kiểm chứng biểu thức đó đúng với mọi $x$.
- 2. Trong trường hợp nghiệm tìm được là số thập phân ta dự đoán $y$ là hàm phân thức theo biến $x$, sẽ giải khi xét bài toán tiếp theo (câu 47-THPTQG2017)
| Nhận xét:
|
Chia sẻ
About TS. Nguyễn Thái Sơn
