BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tính gần đúng tích phân bằng công thức hình thang thực hiện trên bảng tính (Bài 2)
- 25/04/2024
- 72 lượt xem
| Để giám sát sự ổn định của phương pháp này, chúng tôi chọn thêm 1 số ví dụ từ các thầy cô khác. Ví dụ 3: Cho hàm số $y=f(x)$ liên tục trên đoạn $\big[0;\dfrac{\pi}{2}\big]$ sao cho $f(0)=0, f'(x)=2\sin x -3\sin^3x$. Tính tích phân $I=\displaystyle\int_0^{\pi/2}\dfrac{f(x)}{\sin^2x+1}dx $ A. $1-\dfrac{\pi}{3}\qquad \qquad \qquad \qquad$ B. $\dfrac{3\pi}{4}-2\qquad \qquad \qquad \qquad$ C. $1-\dfrac{\pi}{4}\qquad \qquad \qquad \qquad$ D. $\dfrac{\pi}{4}-1$ |
Đặt $g(x)=\dfrac{f(x)}{\sin^2x+1}⇒ g(0)=0$ và $g'(x)=\dfrac{f'(x)(\sin^2x+1)-2\sin x\cos x.f(x)}{(\sin^2x+1)^2}$.
Thu gọn $g'(x)=\dfrac{2\sin x-3\sin^3x}{\sin^2x+1}-\dfrac{\sin 2x}{\sin^2x+1}.g(x)$. Lưu hai biểu thức vào biến nhớ f(x) và g(x):
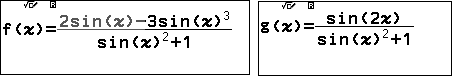
| Ta tính tích phân $I=\displaystyle\int_0^{\pi/2}g(x)dx$. |
Theo công thức xấp xỉ tích phân, ta chia đoạn $[a;b]$ làm 30 phần bằng nhau bởi biến nhớ A. (nhiều hơn sẽ không đủ bộ nhớ trong bảng tính, vì bài này sử dụng hai hàm f(x) và g(x)). 
Mở một bảng tính mới nhập $a=0$ vào $A_1$, $g(a)=0$ vào $B_1$.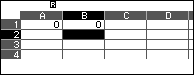 
Đưa con trỏ tới $A_2$ điền công thức (như trong hình), chú ý phạm vi $A_2:A_{30}$, cell $A_{30}$ sẽ chứa giá trị $\dfrac{\pi}{2}$. 
Đưa con trỏ tới $B_2$ điền công thức (như trong hình), chú ý phạm vi $B_2:B_{30}$,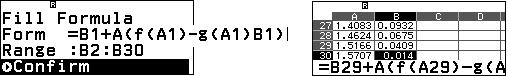 
Đưa con trỏ tới $C_{30}$ thực hiện phép tính như trong hình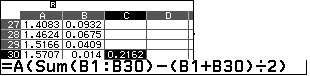 
Vậy $I\approx 0,2162$ so với phương án đúng 
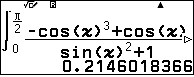
| Lưu ý: Phương pháp xấp xỉ tích phân chỉ nên sử dụng khi không thể tìm được $f(x)$ từ phương trình hàm đã cho. Nếu ta tìm được $f(x)$ bài toán sẽ dễ dàng hơn và kết qủa chính xác hơn. Ví dụ, trong bài này ta tìm được $f(x)=-\cos^3x+\cos x$. Khi đó
$I=$
 |
About TS. Nguyễn Thái Sơn
