Tính gần đúng tích phân bằng công thức hình thang thực hiện trên bảng tính
- 24/04/2024
- 195 lượt xem
| Công thức hình thang: Giả sử ta muốn xấp xỉ tích phân $I=\displaystyle \int_a^bf(x)dx$.
Trong các các tài liệu về giải tích số, giới thiệu công thức: $\color{blue}\bullet\quad $$h=\dfrac{b-a}{n}$, với $n$ là số đoạn được chia trên đoạn $[a;b]$. $\color{blue}\bullet\quad $$x_0=a, x_n=b, x_i=x_0+ih=x_{i-1}+h$ ($i=1,2,3,\dots, n)$. $\color{blue}\bullet\quad $Sai số $\varepsilon < M.\dfrac{b-a}{12}\times h^2$ với $\displaystyle M=\max_{x\in [a;b]}|f''(x)|$. |
Trong các bài toán VDC thi TNTHPT thời gian qua, đề bài không cho biểu thức $f(x)$ mà chỉ cho biểu thức $f'(x)$, Vì vậy ta xấp xỉ $f(x_i)$ bởi công thức vi phân: $$f(x_i)=f(x_{i-1}+h)\approx f(x_{i-1})+hf'(x_{i-1})$$
Trên máy tính Casio fx-880BTG ta thực hiện việc xấp xỉ như sau:
|
Ví dụ 1 (2019): 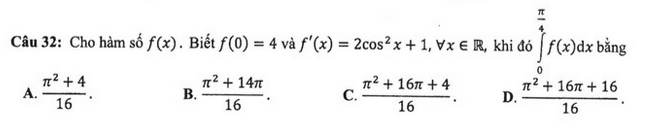
| Chú ý: Đối với học sinh có học lực tốt, các em tìm nguyên hàm của $f'(x)$, đem nguyên hàm thay vào tích phân và thực hiện tính toán trên máy tính. Ở đây ta luyện tập thêm công thức xấp xỉ hình thang, phòng khi gặp một phương trình hàm mà ta không giải được để tìm $f(x)$. |
Lấy $\dfrac{\pi}{4}\div 44$ lưu vào A  .
.
Lưu $f'(x)$ vào $g(x)$ 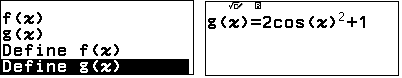
Mở một bảng tính, nhập 0 vào $A_1$, $4$ vào $B_1$ 
Đưa con trỏ tới $A_2$ điền công thức, phạm vi $A_2:A_{45}$  (để gọi được biến nhớ A, bấm vào SHIFT 4. (Theo cách chia đoạn [a;b] thành 45 phần bằng nhau thì $A_{45}$ chứa giá trị $b=\dfrac{\pi}{4}$).
(để gọi được biến nhớ A, bấm vào SHIFT 4. (Theo cách chia đoạn [a;b] thành 45 phần bằng nhau thì $A_{45}$ chứa giá trị $b=\dfrac{\pi}{4}$).
Đưa con trỏ tới $B_2$ điền công thức, phạm vi $B_2:B_{45}$  .
.
Đưa con trỏ tới $C_{45}$ thực hiện phép tính: 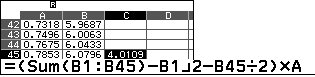
So sánh với phương án C  , ta chọn C.
, ta chọn C.
Ví dụ 2 (2020TK): 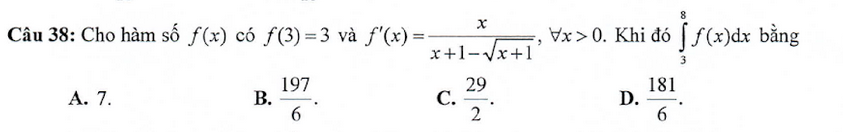
| Chú ý: Đối với học sinh có học lực tốt, các em lấy tử và mẫu nhân cho lượng liên hợp của mẫu, từ đó tìm nguyên hàm của $f'(x)$, đem nguyên hàm thay vào tích phân và thực hiện tính toán trên máy tính. Ở đây ta luyện tập thêm công thức xấp xỉ hình thang, phòng khi gặp một phương trình hàm mà ta không giải được để tìm $f(x)$. |
Vì thuật toán cũ vẫn còn trên bảng tính nên ta chỉ cần thay hàm $g(x)=f'(x)$ mới 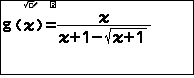 , thay biến A mới
, thay biến A mới  , nhập $A_1=3, B_1=f(3)=3$
, nhập $A_1=3, B_1=f(3)=3$ 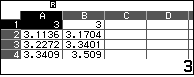 .
.
Kết quả là: 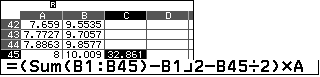 .
.
So sánh với phương án đúng 
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay