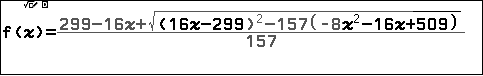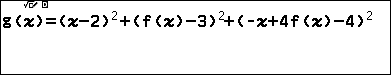BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng MT Casio fx-880BTG giải câu 50 đề thi minh hoạ
- 26/03/2024
- 223 lượt xem
 |
 |
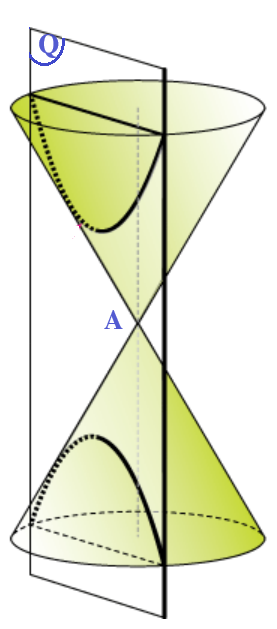Hình nón có đỉnh $A(2;3;0)$, trục của nó đi qua $A$ và vuông góc với mặt phẳng $(P):2x+y+2z-1=0$ vectơ pháp tuyến $\overrightarrow{n}=(2;1;2)$. Vì $d(A,(P))=2$ và đường sinh bằng $5$ nên góc giữa trục và đường sinh của hình nón bằng $\arccos\dfrac25$.
Ta lấy một điểm $X(x;y;z)$ trong không gian. $\overrightarrow{AX}=(x-2;y-3;z)$. Điểm $X$ thuộc mặt nón khi và chỉ khi $\widehat{\left(\overrightarrow{AX}, \overrightarrow{n}\right)}=\arccos\dfrac25.$ Vậy phương trình mặt nón là $$\dfrac25=\dfrac{|2x+y+2z-7|}{3\sqrt{(x-2)^2+(y-3)^2+z^2}}\qquad (1)$$ |
Thay (2) vào (1), bình phương hai vế kết quả và thu gọn:
$$157y^2+2(16x-299)y-8x^2-16x+509=0$$
(việc khai triển và thu gọn không quá phức tạp, chẳng hạn khi thay (2) vào (1) thì tử số thành $3(3y-5)$, đơn giản $3$ cho mẫu.).
Giải phương trình tìm $y$ theo $x$: $$y=\dfrac{299-16x\pm \sqrt{(16x-299)^2-157(-8x^2-16x+509)}}{157}$$
Do tính đối xứng của mặt nón và hyperbol qua điểm $A$ nên chỉ cần chọn một trong hai dấu $\pm$, ta chọn dấu $+$.
Bây giờ ta tính $AM^2=(x-2)^2+(y-3)^2+z^2$ với $x-4y+z+4=0$.
Ta thực hiện trên máy tính Casio fx-880BTG.
|
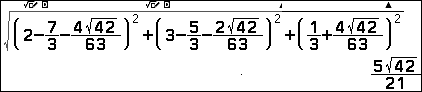
| Nhận xét: Một điều rất thú vị là nhờ máy tính cầm tay ta có thể tìm ra được chính xác $x_{\text{ct}}=\dfrac73+\dfrac{4}{63}\sqrt{42}$ và toạ độ điểm $M$ là $$M\left(\dfrac73+\dfrac{4}{63}\sqrt{42};\dfrac53+\dfrac{2}{63}\sqrt{42};\dfrac13+\dfrac{4}{63}\sqrt{42}\right)$$
Khi đó: $AM=\sqrt{(x_A-x_M)^2+(y_A-y_M)^2+(z_A-z_M)^2}=$ |
About TS. Nguyễn Thái Sơn
