Giải câu 49 đề minh hoạ của BGD và ĐT

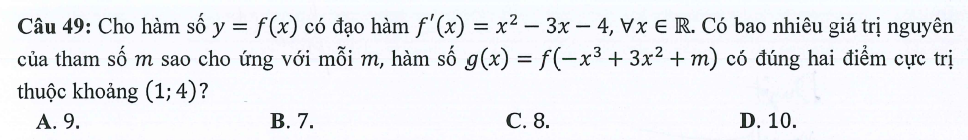Ta có: $g'(x)=(-3x^2+6x)f'(-x^3+3x^2+m)$

$g'(x)=0 ⇔ \left[\begin{array}{ll}-3x^2+6x=0 &(1)\\
f'(-x^3+3x^2+m)=0 &(2)
\end{array} \right.$

Phương trình (1) có đung một nghiệm thuộc khoảng $(1;4)$ đó là $x=2$.

$(2) ⇔ \left[\begin{array}{l}-x^3+3x^2+m=-1\\
-x^3+3x^2+m=4\end{array} \right. ⇔ \left[\begin{array}{l}m=x^3-3x^2-1\\
m=x^3-3x^2+4\end{array} \right.$

Vẽ đồ thị của hai hàm số $y=x^3-3x^2-1$ và $y=x^3-3x^2+4$ trên cùng một hệ trục toạ độ với $x \in [1;4]$.

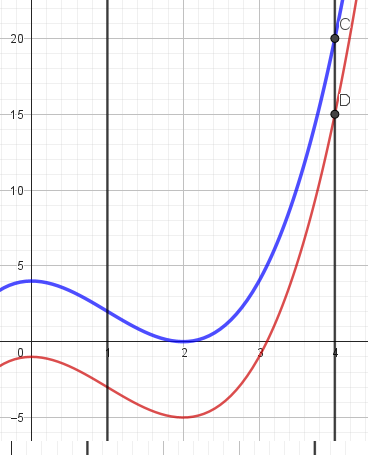
Nhìn vào đồ thị ta thấy:

1. 1. Nếu $m=-5$ phương trình (2) có 1 nghiệm kép $x=2$. Do đó hàm số đã cho chỉ có một điểm cực trị.
2. 2. Nếu $m=-4$ phương trình (2) có 2 nghiệm khác $x=2$. Do đó hàm số đã cho chỉ có ba điểm cực trị.
3. 3. Nếu $m=-3, -2, -1$ phương trình (2) có 1 nghiệm khác $x=2$. Do đó hàm số đã cho có đúng hai điểm cực trị.
4. 3. Nếu $m=0$ phương trình (2) có 1 nghiệm đơn và một nghiệm kép $x=2$. Do đó hàm số đã cho có đúng hai điểm cực trị.



5. 3. Nếu $m$ nguyên và $0<m<15$ phương trình (2) có 2 nghiệm khác $2$. Do đó hàm số đã cho có ba điểm cực trị.
6. 3. Nếu $m=15. 16, 17, 18, 19$ phương trình (2) có 1 nghiệm khác $2$. Do đó hàm số đã cho có đúng hai điểm cực trị.



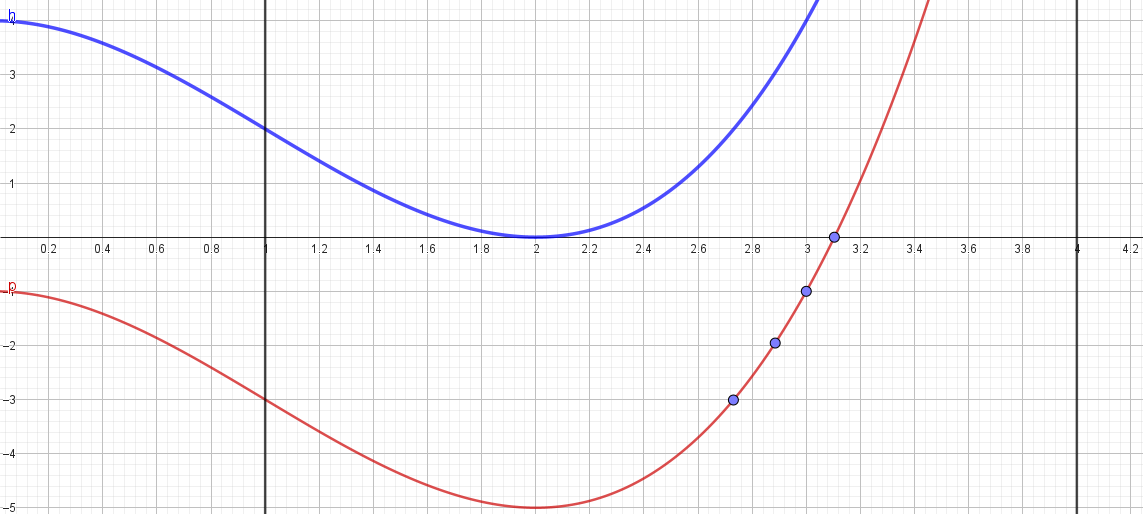
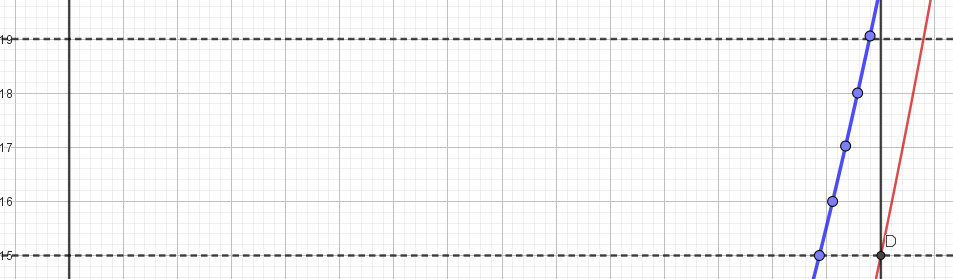
Tổng kết có 9 giá trị của $m$ làm cho hàm số có đúng hai điểm cực trị thuộc khoảng $(1;4)$ đó là:
$$m \in \Big\{-3, -2, -1, 0, 15, 16, 17, 18, 19\Big\}$$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.