BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm k chữ số cuối cùng của số a^n trên bảng tính.
- 26/04/2024
- 76 lượt xem
| Bài toán: Tìm $k$ chữ số cuối cùng của số $a^n$, trong đó $k$ là một số tự nhiên (tối đa $k=5$), $a$ là một số nguyên (đôi khi ta gặp $a$ là số nguyên tố) tối đa bằng $19$ và $n$ là số năm từ $2017$ đến tối đa là $2030$ (các năm thi HSG MTCT TP HCM). |
Chú ý: Nếu $a>19$ và $n>2030$ thuật toán sẽ phức tạp hơn, không phù hợp với bậc THCS.
Để HỌC SINH và GV có thể hiểu được thuật toán chạy trên bảng tính, chúng tôi giải thích cách thực hiện thông qua một ví dụ đơn giản chạy trên màn hình tính toán thông thường (Calculate):
| Ví dụ: Tìm 5 chữ số cuối cùng của số $2^{2024}$ |
Ta có: 
. Vậy $2024=2^5+2^6+2^7+2^8+2^9+2^{10}+8$.
Do đó:
$$2^{2024}=\underbrace{2^{2^5}.2^{2^6}.2^{2^7}.2^{2^8}.2^{2^9}.2^{2^{10}}}_{\text{số sau là bình phương của số trước}}.2^8$$
$2^{2^5}\equiv 67296$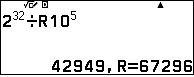 
(tự động lưu R vào biến nhớ F.)
$2^{2^6}\equiv 51616$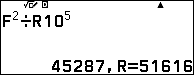 
$2^{2^7}\equiv 11456$ 
(chỉ cần bấm OK/EXE)
$2^{2^8}\equiv 39936$ 
(chỉ cần bấm OK/EXE)
$2^{2^9}\equiv 84096$ 
(chỉ cần bấm OK/EXE)
$2^{2^{10}}\equiv 37216$ 
(chỉ cần bấm OK/EXE)
$2^8\equiv 256$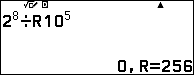 
Lấy hai thừa số đầu tiên nhân cho nhau, tìm dư của phép chia cho $10^5$: 
Nhân tiếp cho thừa số thứ ba: 
Nhân tiếp cho thừa số thứ tư: 
Nhân tiếp cho thừa số thứ năm: 
Nhân tiếp cho thừa số thứ sáu: 
Nhân tiếp cho thừa số cuối cùng và nhận đáp số: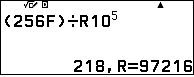 
| Lưu ý: Ở đây $2^{32}$ không quá lớn nên ta bắt đầu từ đây. Tuy nhiên ví dụ $19^{32}$ sẽ cực lớn không sử dụng được, nên ta sẽ tìm đồng dư của nó thông qua $19^4, 19^{8}, 19^{16}$ rồi mới có đồng dư với $19^{32}$ bằng cách bình phương (phần dư) của số đứng trước. |
About TS. Nguyễn Thái Sơn
