Sử dụng bảng tính để tính $(a+b\sqrt3)^n\ (a, b \in \mathbb{R}, n\in \mathbb{N})$ thành $A+B\sqrt3$
- 05/02/2024
- 231 lượt xem
| Để đơn giản và dễ hiểu ta sẽ tính $(2+\sqrt3)^n$ |
Khi $n=1$ ta có: $2+\sqrt3=a_1+b_1\sqrt3$
Khi $n=2$ ta có $(2+\sqrt3)^2=(a_1+b_1\sqrt3).(2+\sqrt3)=2a_1+3b_1+(a_1+2b_1)\sqrt3=a_2+b_2\sqrt3$
……………………………………………………………………………………..
$(2+\sqrt3)^n=2a_{n-1}+3b_{n-1}+(a_{n-1}+2b_{n-1})\sqrt3$
Mở một bảng tính, nhập 2 vào A1, 1 vào B1 và $\sqrt3$ vào C1.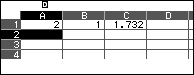
Ta điền công thức sau vào A2/B2 sau đó chọn phạm vi A2:A5 / B2: B5 để tính $(2+\sqrt3)^n$ với $n=2,3,4,5$.
A2=2A1+3B1; B2=A1+2B1
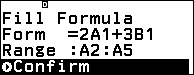
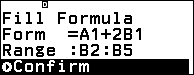
Kết quả: 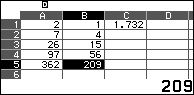
| Áp dụng Biết $2+\sqrt3$ là một nghiệm của đa thức $x^5+ax^4+bx^3-30x^2+30x-6\ (a, b \in \mathbb{Q})$. Hãy tìm $a$ và $b$. |
Thay $x=2+\sqrt3$ vào đa thức ta được kết quả là một số có dạng $A+B\sqrt3$. Vì $2+\sqrt3$ là nghiệm nên $A+B\sqrt3=0$. Vì $a, b$ là các số hữu tỉ nên $A=B=0$.
Dựa vào kết quả trên bảng tính, ta có $$\left\{\begin{array}{l}A=362+97a+26b-30.7+30.2-6=0\\ B=209+56a+15b-30.4+30.1=0\end{array}\right.$$
Giải hệ phương trình trên máy tính:
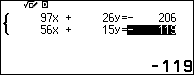


Vậy $$a=-4, b=7$$
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay