BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Phần nguyên của số $(2+\sqrt3)^{32}$
- 02/02/2024
- 182 lượt xem
Nếu ta thực hiện phép tính $(2+\sqrt3)^{32}$ trên máy tính Casio fx-880BTG nó sẽ xuất ra kết quả được làm tròn thành số nguyên:  2005956546822746114 .
|
| Nguyên nhân được làm tròn là vì số đã cho là một số thập phân vô hạn không tuần hoàn mà phần thập gồm nhiều hơn 4 chữ số 9 hoặc gồm nhiều hơn 4 chữ số 0 liên tiếp. Chú ý: Máy tính Casio fx-880BTG có khả năng hiển thị 23 chữ số trong đó phần nguyên đã gồm 19 chữ số. |
Để có một kết quả chính xác cho số $(2+\sqrt3)^{32}$ ta thao tác như sau:
Tính $(2+\sqrt3)^{16}=A+x$, trong đó $A$ là phần nguyên (lưu vào biến A) và $x$ là phần thập phân (lưu vào biến x).
Khi đó: $(2+\sqrt3)^{32}=A^2+x^2+2Ax$
Phần nguyên của $(2+\sqrt3)^{32} \ \text{bằng}\ A^2+[2Ax]+[x^2+y]=$ 2005956546822746113 ($y$ là phần thập phân của $2Ax$)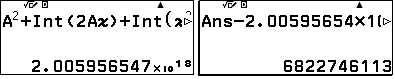
.
Phần thập phân của $(2+\sqrt3)^{32}$ bằng phần thập phân của $x^2+y $ bằng $0,999\dots $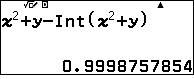 
| Nhận xét: Tuy máy tính Casio fx-880BTG có khả năng hiển thị 23 chữ số, nhưng đó là kết quả của những phép tính về số nguyên. Với các phép tính là số vô tỉ, khả năng hiển thị được 23 chữ số trong nhiều trường hợp không thực hiện được do máy tính phải làm tròn số nhiều lần. Ở đây ta đã thực hiện được 22 chữ số: $$(2+\sqrt3)^{32}=2005956546822746113,999\dots $$ Muốn có kết quả chính xác hơn ta phải dùng tới các máy vi tính. Khi đó ta có thể có nhiều chữ số hơn, cụ thể $$(2+\sqrt3)^{32}=2005956546822746113,\underbrace{999999999999999999}_{18\ \text{chữ số}\ 9}5014847148190175768903495\dots $$ |
Chia sẻ
About TS. Nguyễn Thái Sơn
