BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm k chữ số cuối cùng của số a^n trên bảng tính (tiếp theo).
- 26/04/2024
- 329 lượt xem
|
Để dễ hiểu bài này, các bạn nên đọc bài dẫn nhập trước, tại đây.
|
| Sau đây ta xây dựng thuật toán chạy trên bảng tính để tìm $k$ chữ số cuối cùng của số $a^n$. Bạn đọc phải đọc bài trước của bài này mới hiểu thuật toán. Ưu điểm của cách chạy trên bảng tính đó là ta có thể thay $k,a,n$ bằng bộ ba khác trong phạm vi giám sát được $1\leqslant k \leqslant 5$; $2\leqslant a\leqslant 19$; $2017\leqslant n \leqslant 2030$. |
Trên bảng tính ta thực hiện lại $2^{2024}$ sau đó tuỳ biến cho các bộ ba khác.
Mở một bảng tính mới nhập $a=2$ vào $B_1$, $n=2024$ vào $C_1$, $k=5$ vào $D_1$, đưa con trỏ tới $A_{11}$ thực hiện phép tính $C_1-2016$ (đúng ra $C_1$ phải cố định, nhưng chỉ dùng 1 lần nên không cần dấu $\$$.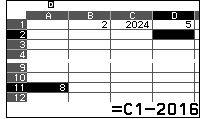 
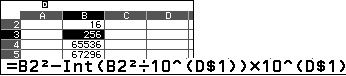
Đưa con trỏ tới $B_2$ tìm dư của phép chia $(B_1)^{2^2}$ cho $D_1$ mục đích là để chút nửa tìm đồng dư của $(B_1)^{2^5}$, vì chỉ sử dụng một lần nên không cần cố định các tham chiếu.
Đưa con trỏ tới $B_3$ điền công thức như trên hình, phạm vi $B_3:B_{10}$ để tìm đồng dư của $(B_i)^2$ ($i=3, 4,$ $5, 6, 7, 8, 9, 10$, hãy nhớ số sau là bình phương số trước).
Tính riêng cho $B_{11}$ dùng một lần không cần cố dịnh các tham chiếu: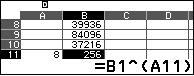 
Đưa con trỏ tới $C_6$, lấy hai đồng dư đầu tiên nhân cho nhau và tìm dư của phép chia của nó cho $10^5$ (xem lại bài trước):
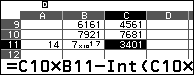
Đưa con trỏ tới $C_7$ điền công thức như trên hình, phạm vi $C_7:C_{11}$ 
C11 chứa đáp số của bài toán:  |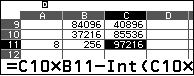
Tuỳ biến:
1) Xác định 5 chữ số cuối cùng của số $3^{2025}$
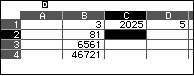
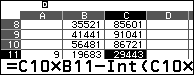
2) Xác định 5 chữ số cuối cùng của số $5^{2026}$
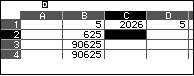
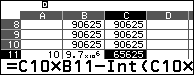
3) Xác định 4 chữ số cuối cùng của số $19^{2030}$
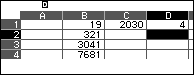
Giá trị đúng của số $19^{2030}$ là:
About TS. Nguyễn Thái Sơn
