BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Diện tích của hình viên phân
- 21/02/2024
- 227 lượt xem
| Hình viên phân là một phần của hình tròn giới hạn bởi một cung và dây căng cung. |
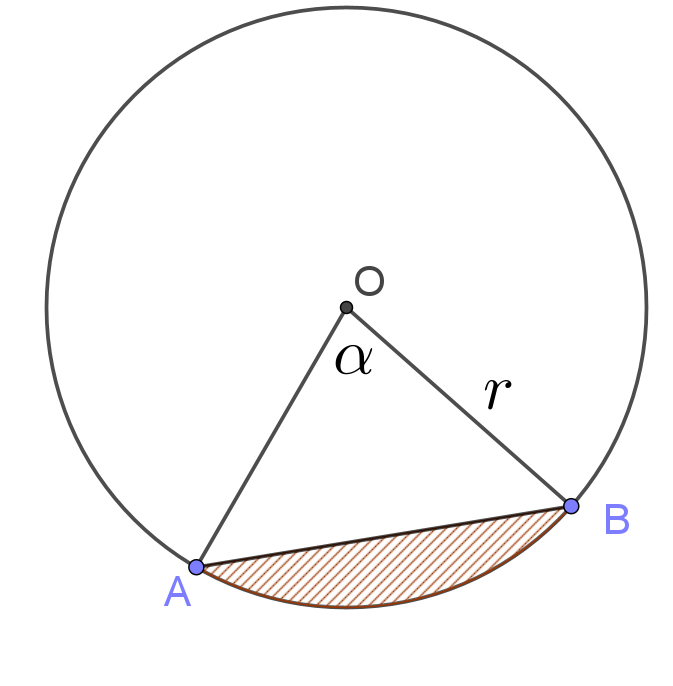
| Diện tích của hình viên phân (cung AB) bằng diện tích của hình quạt tròn $OAB$ trừ cho diện tích tam giác $OAB$.$$S_{\text{vp AB}}=S_{\text{hình tròn}}.\dfrac{\alpha}{360} -S_{OAB}=\dfrac{r^2}{2}\left(2\pi.\dfrac{\alpha}{360}-\sin\alpha\right)$$ |
Áp dụng: Tính (chính xác đến 3 chữ số thập phân sau dấu phẩy) diện tích phần tô đen (như hình bên)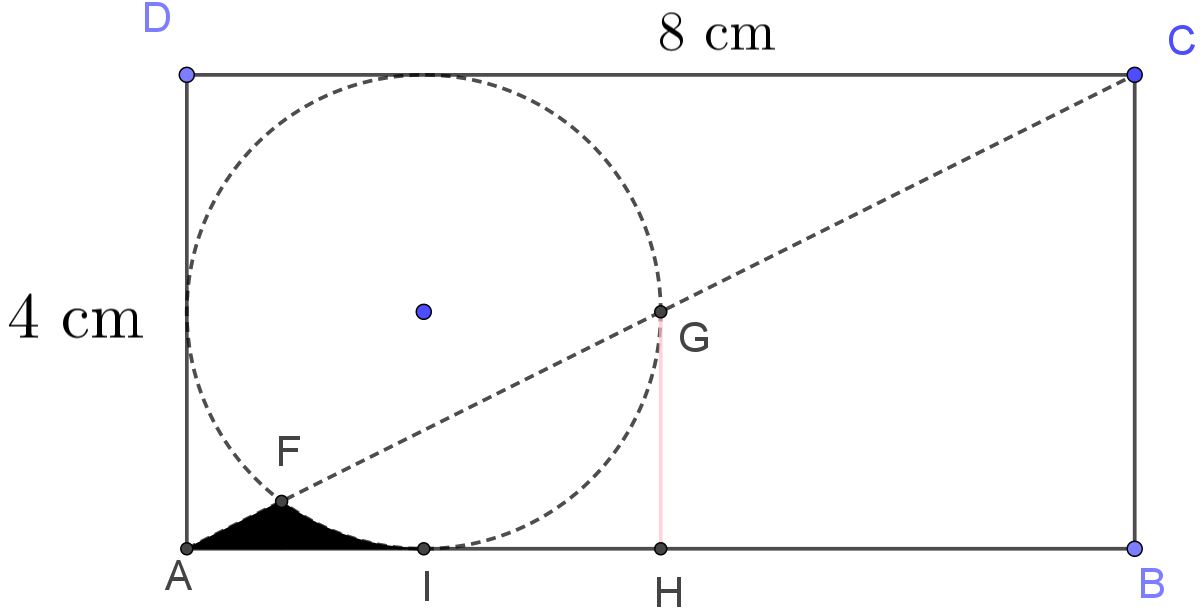 biết hình chữ nhật ABCD có cạnh $AB = 8$ cm, $BC = 4$ cm và đường tròn (O) tiếp xúc với ba cạnh của hình chữ nhật. |
Diện tích của phần tô đen bằng diện tích tam giác $AGH$ trừ đi diện tích tam giác cong $IGH$ (phần phía ngoài đường tròn của tam giác $IGH$) trừ thêm diện tích hình viên phân cung $FG$.
Vậy $$S=\dfrac{1}{2}.2.4-\dfrac{S_{\text{hv}\ HADH’}-S_{\text{hình tròn}}}{4}-\dfrac{r^2}{2}\left(2\pi.\dfrac{\alpha}{360}-\sin \alpha\right)$$
$H’$ là đỉnh thứ tư của hình vuông và $\alpha =180^\circ-2\arctan\dfrac12$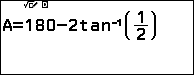 
.
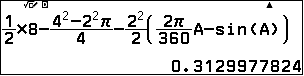
Chia sẻ
About TS. Nguyễn Thái Sơn
