Tính nhanh thể tích khối tứ diện khi biết 6 cạnh

Cho khối tứ diện như hình vẽ: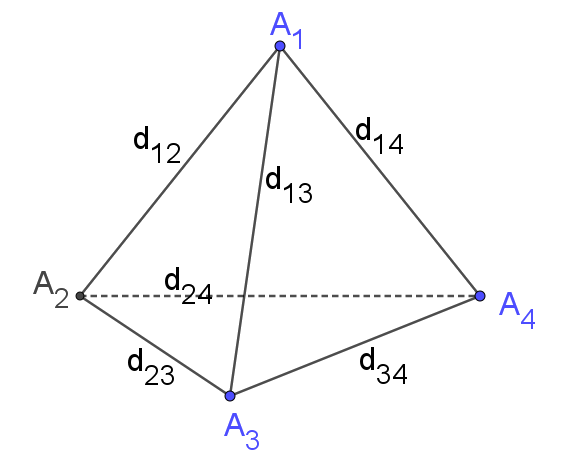

Xây dựng ma trận vuông cấp 3 theo từng bước như sau:
$\left(\begin{array}{ccc}
2d_{12}^2&\color{red}\bullet&\\
\color{red}\bullet&2d_{13}^2&\\
&&2d_{14}^2
\end{array}\right)\rightarrow
\left(\begin{array}{ccc}
2d_{12}^2&d_{12}^2+d_{13}^2-d_{23}^2&\color{blue}\bullet\\
d_{12}^2+d_{13}^2-d_{23}^2&2d_{13}^2&\\
\color{blue}\bullet&&2d_{14}^2
\end{array}\right)$

(tổng bình phương hai cạnh tam giác $A_1A_2A_3$ trừ bình phương cạnh thứ ba)

$\rightarrow
\left(\begin{array}{ccc}
2d_{12}^2&d_{12}^2+d_{13}^2-d_{23}^2&d_{12}^2+d_{14}^2-d_{24}^2 \\
d_{12}^2+d_{13}^2-d_{23}^2&2d_{13}^2&\color{magenta}\bullet\\
d_{12}^2+d_{14}^2-d_{24}^2&\color{magenta}\bullet&2d_{14}^2
\end{array}\right)$

(tổng bình phương hai cạnh tam giác $A_1A_2A_4$ trừ bình phương cạnh thứ ba)

$\rightarrow
A=\left(\begin{array}{ccc}
2d_{12}^2&d_{12}^2+d_{13}^2-d_{23}^2&d_{12}^2+d_{14}^2-d_{24}^2 \\
d_{12}^2+d_{13}^2-d_{23}^2&2d_{13}^2&d_{13}^2+d_{14}^2-d_{34}^2\\
d_{12}^2+d_{14}^2-d_{24}^2&d_{13}^2+d_{14}^2-d_{34}^2&2d_{14}^2
\end{array}\right)$

(tổng bình phương hai cạnh tam giác $A_1A_3A_4$ trừ bình phương cạnh thứ ba).

Sắp các cạnh theo thứ tự:$$AB=5, AC=2\sqrt2, AD=\sqrt{22}, BC=\sqrt{13}, BD=3\sqrt3, CD=\sqrt{10}$$
 

Chú ý: $d_{12}^2+d_{13}^2-d_{23}^2=2.d_{12}d_{13}.\cos\widehat{A_2A_1A_3}$
 

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.