Giải hệ phương trình đồng dư bằng định lý phần dư Trung Hoa
- 26/04/2024
- 141 lượt xem
Định lý phần dư Trung Hoa (hay còn gọi là “bài toán Hàn Tín điểm binh”).
| Xét hệ phương trình: $$\left\{ \begin{array}{l} x \equiv a_1 \quad (\kern-.2em\mod m_1) \\ x \equiv a_2 \quad (\kern-.2em\mod m_2) \\ x \equiv a_3 \quad (\kern-.2em \mod m_3) \\ \end{array}\right.$$ trong đó $m_1, m_2, m_3$ đôi một nguyên tố cùng nhau. |
|
Hệ phương trình đồng dư nói trên có nghiệm duy nhất là: $x=a_1y_1z_1+a_2y_2z_2+a_3y_3z_3\quad (\kern-.5em\mod m)$
với $m=m_1.m_2.m_3$, $y_1=\dfrac{m}{m_1}$, $y_2=\dfrac{m}{m_2}$, $y_3=\dfrac{m}{m_3}$ và $z_i$ là nghịch đảo của $y_i$ theo mô-đu-lô $m_i$, nghĩa là $z_i.y_i \equiv 1\ (\kern-.5em\mod m_i)$ ($i=1,2,3$). |
Cách đây hai năm, trên BITEXEDU chúng tôi đã trình bày cách dùng bảng tính để tìm nghịch đảo mô-đu-lô. Hôm nay chúng tôi nhắc lại, theo hướng “dễ nhớ hơn”, bằng cách nói trước thực hành sau.
Giả sử ta muốn tìm nghịch đảo theo mô-đu-lô $m_1=7741$ của số $y_1=$3937 , ta nhập $m_1, y_1, 0, 1$ lần lượt vào $A_1, B_1, C_1, D_1$. 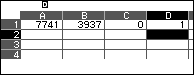
Tiếp theo ta dời số liệu từ cột B “chéo xuống” cột A, dời số liệu từ cột D “chéo xuống” cột C như minh hoạ 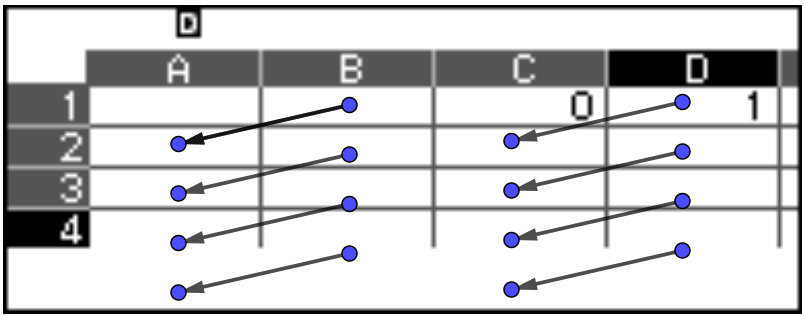
Trên cột B từ $B_2:B_{20}$ ta tìm dư của phép chia cột A cho cột B theo dòng tương ứng. Ví dụ tại dòng 2 phép tính là:$A_1-B_1$.Int($A_1\div B_1$).
Trên cột D từ $D_2:D_{20}$ ta thực hiện phép tính $C-D$.Int($A\div B$) (dòng tương ứng), ví dụ dòng 2 phép tính là: $C_1-D_1$.Int($A_1\div B_1$).
Quan sát kết quả, ở dòng nào mà cột B là $1$ thì tại dòng đó, cột D sẽ là nghịch đảo cần tìm nếu nó là số dương. Nếu nó là số âm ta cộng cho $k$ lần $m_1$ (với $k$ nhỏ nhất mà kết quả là dương), giá trị dương này sẽ là nghịch đảo cần tìm.
Bài luyện tập – bài thi HSG MTCT THCS
Xét hệ phương trình đồng dư
$$\left\lbrace\begin{array}{llll}
x & \equiv & 2017 & (\text{mod} \ 7741)& \\
x & \equiv & 2013 & (\text{mod} \ 2017)& \\
x & \equiv & 2011 & (\text{mod} \ 2013)
\end{array} \right.
$$

Vì $7741, 2017,2013$ nguyên tố cùng nhau nên ta có thể sử dụng Định lý Phần dư Trung Hoa. Khi đó nghiệm duy nhất của hệ phương trình là $$x=2017.2017.2013z_1+2013.2013.7741z_2+2011.7741.2017z_3\quad (\kern-.51em\mod 2017.2013.2011)\qquad (*)$$
trong đó $z_1, z_2, z_3$ lần lượt là nghịch đảo của $2017.2013$ theo mô-đu-lô $7741$,của $2013.7741$ theo mô-đu-lô $2017$ và của $7741.2017$ theo mô-đu-lô $2013$.
Bây giờ ta đi tìm $z_1$ sau đó tuỳ biến sẽ có $z_2$ và $z_3$.
Lần lượt nhập $7741, 2017\times 2013, 0 ,1$ lên dòng 1 như hình: 
Dời “chéo xuống” số liệu từ cột B sang cột A và từ cột D sang cột C (chọn phạm vi 20 dòng) bằng cách đưa con trỏ tới $B_2$ điền công thức và đưa con trỏ tới $C_2$ điền công thức như hình:

Đưa con trỏ tới $B_2$ điền công thức, phạm vi $B_2:B_{20}$ để tìm dư của phép chia $A_i$ cho $B_i\quad (i=1,2,\dots, 20)$, bỏ qua thông báo lỗi (chia cho $0$) như hình:

Đưa con trỏ tới $D_2$ điền công thức, phạm vi $D_2:D_{20}$ thực hiện phép tính như trong hình, bỏ qua thông báo lỗi (chia cho $0$):

Duyệt cột $B$ thấy $B_{10}=1$ mà $D_{10}=-291<0$ nên $z_1=-291+7741=7450$. 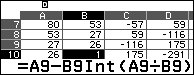
Bây giờ ta tuỳ biến giá trị nhập vào để có $z_2$ và $z_3$. Đưa con trỏ vào $A_1$ nhập $2017$, vào $B_1$ nhập $2013.7741$, bỏ qua thông báo lỗi (chia cho $0$) (hình bên trái), sau đó duyệt cột $B$ thấy $B_9=1$ nên $z_2=D_9=165$.

Lại đưa con trỏ vào $A_1$ nhập $2013$, vào $B_1$ nhập $7741.2017$, bỏ qua thông báo lỗi (chia cho $0$) (hình bên trái), sau đó duyệt cột $B$ thấy $B_{12}=1$ mà $D_{12}=-89<0$ nên $z_2=-89+2013=1924$.

Đem $z_1, z_2, z_3$ thay vào công thức (*) ở trên, ta có:
$$x = a_1y_1z_1+a_2y_2z_2+a_3y_3z_3 + k m_1m_2m_3 = 126598780950343+31430170761k, k \in \mathbb{Z}$$
Vì $x$ lớn nhất và có 14 chữ số nên $k$ lớn nhất thoả $k<$  . Vậy $k=-847$. Do đó số cần tìm là $$x=126598780950343+31430170761\times (-847)=99977426315776$$
. Vậy $k=-847$. Do đó số cần tìm là $$x=126598780950343+31430170761\times (-847)=99977426315776$$
| Câu 1: Kỳ thi HSG MTCT TP HCM 17/01/2016 |
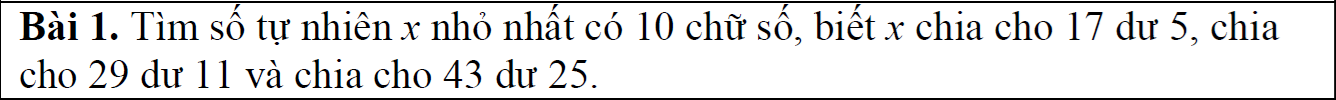 |
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay