BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Bổ sung về một bài toán dãy số quy nạp
- 02/03/2024
- 183 lượt xem
| Cho dãy số $\qquad \qquad a_1=0, a_{n}=\dfrac{(n-1)n}{(n+1)(n+2)}(a_{n-1}+1)\quad \forall n \geqslant 2.$ Tính $a_{2024}$ |
Lần trước chúng tôi giới thiệu số hạng tổng quát, dạng chưa thu gọn và dạng thu gọn:
| $$a_1=0, a_n=\dfrac{(n-1)(2n+1)}{10(n+1)}\ (n \geqslant 2)$$ |
Bài viết này trình bày lộ trình dẫn đến kết quả đó.
Ta tìm 10 số hạng đầu tiên của dãy số để từ đó dự đoán số hạng tổng quát.
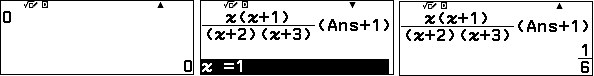$\left(a_2=\dfrac{T_2}{M_2}\right)$
$\left(a_3=\dfrac{T_3}{M_3}\right)$
$\left(a_4=\dfrac{T_4}{M_4}\right)$
$a_5=\dfrac{77}{105}$
$a_6=\dfrac{182}{196}$
$a_7=\dfrac{378}{336}$
$a_8=\dfrac{714}{540}$
$a_9=\dfrac{1254}{825}$
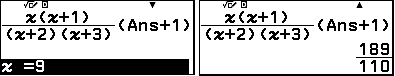$a_{10}=\dfrac{2079}{1210}$
| Ta dự đoán $a_n=\dfrac{T_n}{M_n}$ trong đó $T_n=T_{n-1}+M_{n-1}\quad (1)$ và $M_n=\dfrac{(n+1)(n+2)}{(n-1)n}.M_{n-1}\quad (2)$. |
Dựa vào biểu thức quy nạp (2) ta tính được : $M_n=\dfrac{n(n+1)^2(n+2)}{12}$.
Dựa vào biểu thức quy nạp (1) ta tính được : $T_n=\dfrac{n(2n^4+5n^3-5n-2)}{120}$.
Từ đó suy ra $$a_n=\dfrac{(n-1)(2n+1)}{10(n+1)}\ (n \geqslant 2)$$
Việc chứng minh $a_n$ thoả yêu cầu bài toán không khó, dành cho độc giả.
About TS. Nguyễn Thái Sơn
