Sử dụng PPTĐ trong không gian $Oxyz$

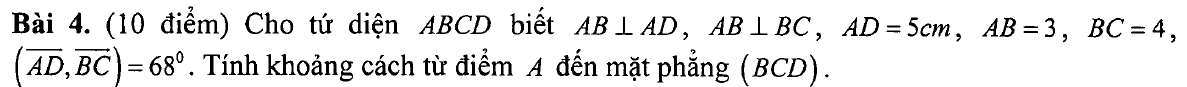
Vì $BA\perp BC$ và $BA\perp AD$ nên có thể vẽ thêm $E, F$ như hình vẽ để có một hình lăng trụ đứng.

Chọn hệ trục toạ độ gốc $O \equiv B$, tia $Ox$ đi qua $C$, tia $Oz$ đi qua $A$, tia $Oy$ vẽ trong mặt phẳng $(BCE)$ để ba tia $Ox, Oy, Oz$ lập thành tam diện thuận (theo quy ước cách chọn hệ trục toạ độ $Oxyz$). Chọn 1 đvd = 1 cm.

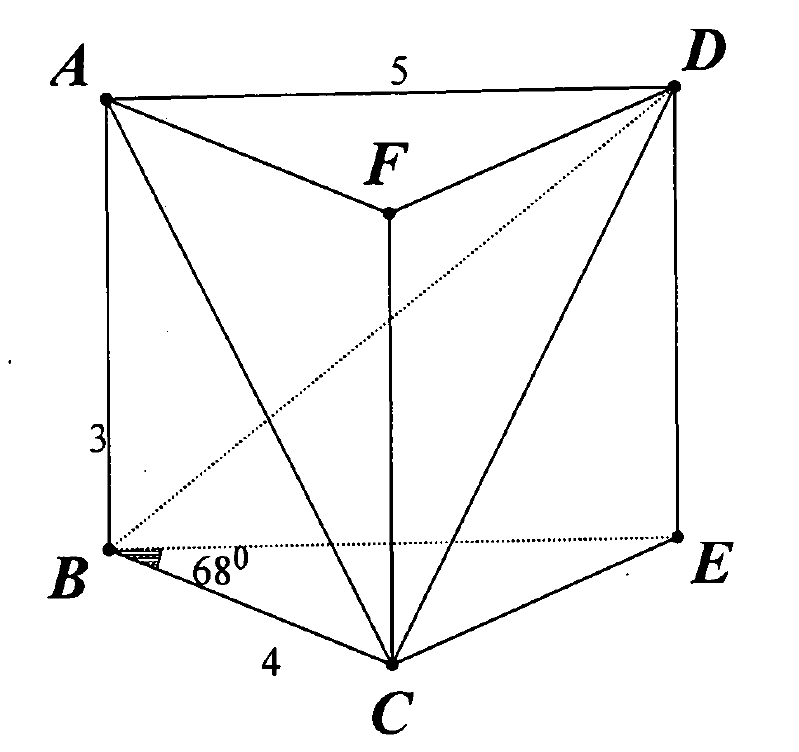
Khi đó $$B(0;0;0), C(4;0;0), A(0;0;3), D(x_E;y_E;3)$$ trong đó $x_E, y_E$ là toạ độ Đề-các trong mặt phẳng $Oxy$ của điểm $E$ có toạ độ cực $(5, 68^\circ)$.

Bấm CATALOG
 
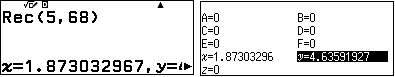, tự động lưu $x,y$ vào các biến nhớ x, y.
 

Vì mặt phẳng $(BCD)$ chứa trục hoành và không trùng với mặt phẳng toạ độ nên phương trình có dạng $By+Cz=0, (B\ne 0, C\ne 0)$, chọn $C=1$ suy ra $B=-\dfrac{z_D}{y_D}$
(lưu $B$ vào biến nhớ B.)
 

Phương trình mặt phẳng $(BCD)$ là $By+z=0$, do đó $d(A, (BCD))$ thực hiện như sau:
 

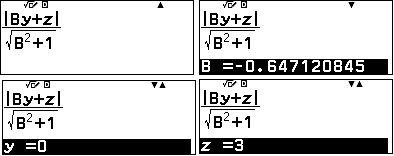
Kết quả:

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013).