BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải bài toán phức tạp HHKG mà không vẽ hình (2)
- 06/03/2024
- 564 lượt xem
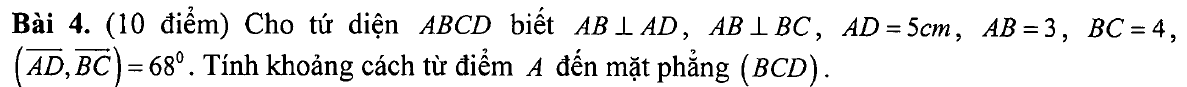
| Trước hết ta tính thêm 3 cạnh để tứ diện có đủ 6 cạnh. |
$$BD=\sqrt{AB^2+AD^2}=\sqrt{34}, \quad AC=\sqrt{BA^2+BC^2}=5$$
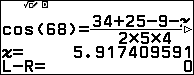
Ta lần lượt lưu các cạnh của khối tứ diện vào 6 biến nhớ với quy ước đặt tên như sau:
$\color{blue}\bullet $ Ba cạnh của tam giác $ABC$ lần lượt đặt tên là $a=BC, b=CA, c=AB$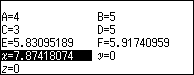 
$\color{blue}\bullet $ $d, e, f$ lần lượt là cạnh đối của các cạnh $a, b, c$.
$$d(A, (BCD))=\dfrac{3V_{ABCD}}{S_{BCD}}$$
trong đó: $V_{ABCD}=\sqrt{\dfrac{\det A}{288}}\quad $ 
, $S_{BCD}=\sqrt{p(p-a)(p-e)(p-f)}$ với $p=\dfrac{a+e+f}{2}$ lưu vào 
(Vì bài toán chọn tam giác $BCD$ làm đáy nên sử dụng ba cạnh $a, e, f$ để tìm diện tích).
$V_{ABCD}=$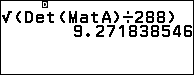 
$S_{BCD}=$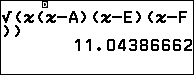 
$d(A, (BCD))=$ 
| Ma trận A được thiết lập như sau:
$a_{11}=2AB^2, a_{22}=2AC^2, a_{33}=2AD^2$ (ba cạnh xuất phát từ đỉnh của tứ diện) $a_{12}=a_{21}=AB^2+AC^2-BC^2$ $a_{13}=a_{31}=AB^2+AD^2-BD^2\qquad $ (thực ra rất dễ nhớ) $a_{23}=a_{32}=AC^2+AD^2-CD^2$ |
About TS. Nguyễn Thái Sơn
