Diện tích của trăng lưỡi liềm
- 19/02/2024
- 171 lượt xem
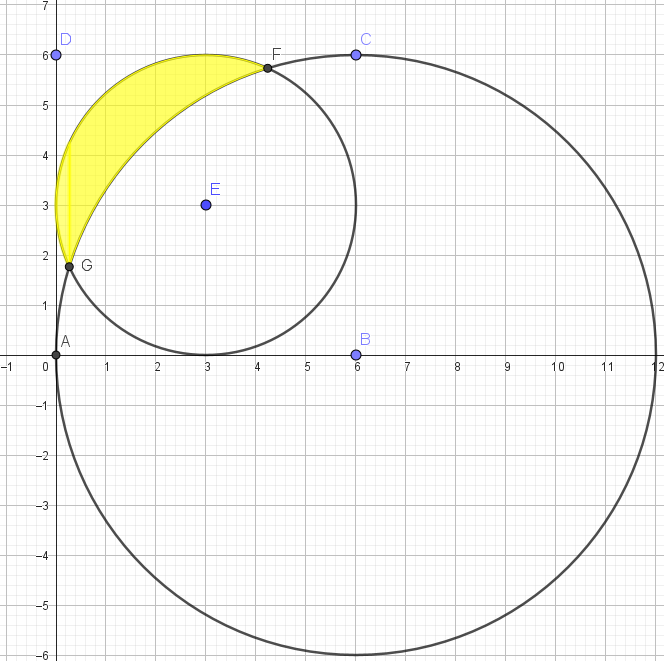
| Bài toán. Trong mặt phẳng $Oxy$ cho hai điểm $B(6;0)$ và $E(3;3$. Đường tròn tâm $B$ bán kính 6 và đường tròn tâm $E$ bán kính 3 cắt nhau tại hai điểm $F$ và $G$. Tìm diện tích của phần tô màu vàng như trong hình vẽ. |
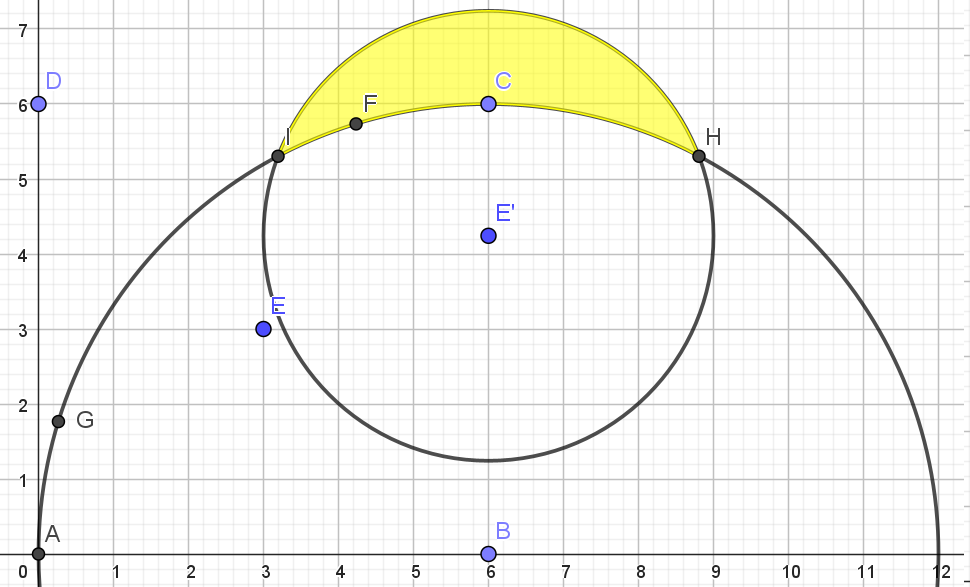
Lấy $B$ làm tâm, quay đường tròn tâm $E$ bán kính 3 một góc $45^\circ$ (theo chiều kim đồng hồ) ta được ảnh của nó là đường tròn có phương trình $y=3\sqrt2\pm \sqrt{9-(x-6)^2}$. Diên tích của hình phẳng phải tính bằng diện tích hình phẳng mới như hình vẽ.
Hoành độ giao điểm là nghiệm của phương trình:$$3\sqrt2+\sqrt{9-(x-6)^2}=\sqrt{36-(x-6)^2}$$
Lưu VT và VP của phương trình lần lượt vào f(x) và g(x) của MÁY TÍNH Casio fx-880BTG:
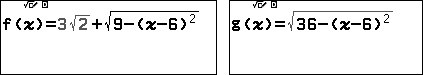
Dùng Solver giải phương trình lần lượt lưu nghiệm vào A và B: 
Khi đó diện tích cần tìm:
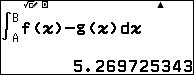
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay