Điều đặc biệt về một bài toán tiếp tuyến của hàm số bậc 3
- 15/02/2024
- 401 lượt xem
| Bài toán Cho hàm số $y=x^3+ax+b \ (a, b \in \mathbb{R})$ (không có số hạng chứa $x^2$) có đồ thị $(C)$. Một điểm $M_1$ nằm trên ($C)$ có hoành độ bằng $x_1>0$. Tiếp tuyến của đồ thị hàm số $(C)$ tại $M_1$, cắt $(C)$ tại $M_2$, và có hoành độ $x_2$. Tiếp tuyến của đồ thị hàm số $(C)$ tại $M_2$, cắt $(C)$ tại $M_3$, có hoành độ độ $x_3$ … Cứ tiếp tục như thế, tiếp tuyến của đồ thị hàm số tại điểm $M_{n-1}$, cắt đồ thị hàm số tại điểm $M_n$ có hoành độ $x_n$. Tìm $n$ để $x_n$ là số một số tự nhiên có $m$ chữ số, |
Phương trình tiếp tuyến của $(C)$ tại $M_1$: $d_1: y=k_1(x-x_1)+y_1$, trong đó $k_1=y'(x_1), y_1=y(x_1)$.
Phương trình hoành độ giao điểm của $(C)$ và $d_1$: $$x^3+ax+b=k_1(x-x_1)+y_1\qquad (1) $$
Vì phương trình này có nghiệm kép $x=x_1$ nên lập sơ đồ Horner ta tìm được $x_2$:

$(1) ⇔ (x-x_1)^2(x+2x_1)=0 ⇔ x=x_1\ \vee\ x=-2x_1 $.
Vậy $x_2=-2x_1$.
Tiếp tục như thế ta có $x_n=-2x_{n-1}$. Từ đó suy ra $x_n=(-2)^{n-1}x_1$ (chú ý dãy số $(x)_n$ là cấp số nhân).
Vì $x_n$ là số tự nhiên nên $n$ là số tự nhiên lẻ. Khi đó $x_n=2^{n-1}.x_1$. Ngoài ra $x_n$ có $m$ chữ số khi và chỉ khi
$[\log x_n]=m-1 ⇔ [(n-1)\log 2+\log x_1] =m-1$.
Để giải phương trình “phần nguyên” này ta tìm số tự nhiên (lẻ) nhỏ nhất $n$ thoả bất phương trình $(n-1)\log 2+\log x_1 \geqslant m-1$.
Áp dụng bằng số: $x_1=3, m=2024$ ta có $n \geqslant x$ 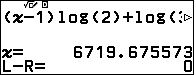 . Vậy $n=6721$. . Vậy $n=6721$. |
| Điều “đặc biệt” của bài toán này là dễ dàng giải được phương trình (1) với số liệu “mơ hồ” . |
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay