BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tích có hướng của 4 vectơ
- 20/07/2021
- 145 lượt xem
Một ưu điểm của máy tính CASIO fx-580VN X đó là có thể nhập vào 4 vectơ và tính toán trực tiếp với 4 vectơ đó.
Bài toán
và $d_2: \dfrac{x-x_1}{b_1}=\dfrac{y-y_1}{b_2}=\dfrac{z-z_1}{b_3}$.
Hãy viết phương trình đường thẳng đi qua $M$ và cắt cả hai đường thẳng $d_1, d_2$.
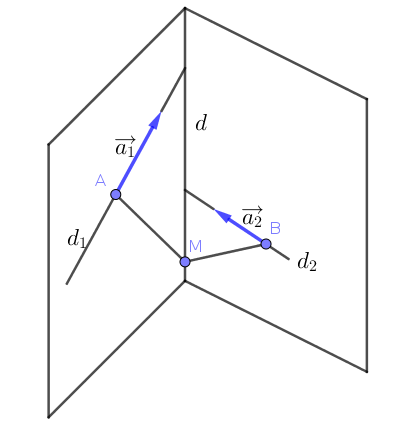
Đường thẳng $d$ là giao tuyến của hai mặt phẳng: $\text{mp}(d,d_1)$ và $\text{mp}(d,d_2)$.
$\text{mp}(d,d_1)$ có cặp vectơ chỉ phương là $\overrightarrow{a_1}, \overrightarrow{MA}$ nên vectơ pháp tuyến của nó là $\overrightarrow{a_1} \times \overrightarrow{MA}$.
$\text{mp}(d,d_2)$ có cặp vectơ chỉ phương là $\overrightarrow{a_2}, \overrightarrow{MB}$ nên vectơ pháp tuyến của nó là $\overrightarrow{a_2} \times \overrightarrow{MB}$.
Vậy vectơ chỉ phương của $d$ là:
$$(\overrightarrow{a_1} \times \overrightarrow{MA})\times (\overrightarrow{a_2} \times \overrightarrow{MB})$$
Áp dụng
$$d_1:\dfrac{x+1}{3}=\dfrac{y+3}{-2}=\dfrac{z-2}{-1}, \quad d_2:\dfrac{x-2}{2}=\dfrac{y+1}{3}=\dfrac{z-1}{-5}$$
mẹo: Muốn tìm toạ độ vectơ $\overrightarrow{AM}$ ta thay toạ độ của $M$ vào các tử số của phương trình đường thẳng.
mẹo: Muốn tìm toạ độ vectơ $\overrightarrow{BM}$ ta thay toạ độ của $M$ vào các tử số của phương trình đường thẳng.
Thực hiện phép tính 
chia vectơ đáp số cho $104$ 
Vậy phương trình đường thẳng cần tìm là $$\dfrac{x+4}{3}=\dfrac{y+5}{2}=\dfrac{z-3}{-1}$$
About TS. Nguyễn Thái Sơn
