Tích vectơ kép của ba vec tơ và ứng dụng

Bài toán

Nhận xét

1. 1. Vectơ $\overrightarrow{u}$ vuông góc với vectơ $\overrightarrow{a}\times \overrightarrow{b}$ và vuông góc với vectơ $\mathbf{\overrightarrow{c}}$
2. 2. Vì thứ tự của 3 vectơ là quan trọng nên vectơ nào chắc chắn vuông góc với vectơ $\overrightarrow{u}$ ta liệt kê cuối cùng. Nghĩa là trong ba vectơ chỉ có một vectơ vuông góc với vectơ $\overrightarrow{u}$, vectơ đó ta liệt kê cuối cùng khi nhập số liệu vào máy tính Casio.

Ứng dụng

 
 
 
 
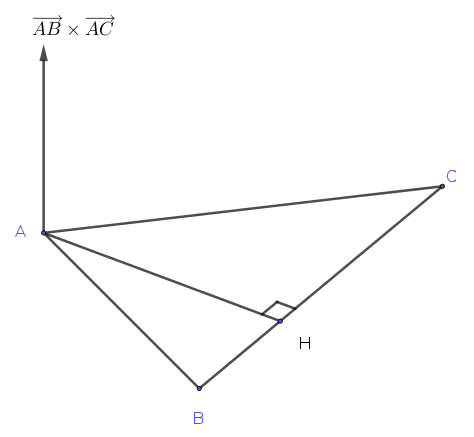
Đường cao $AH$ của tam giác $ABC$ vuông góc với hai vectơ:

$\overrightarrow{AB}\times \overrightarrow{AC}\quad $ và $\quad \overrightarrow{BC}$

Vậy vectơ chỉ phương của đường cao $AH$ là $\overrightarrow{AB}\times \overrightarrow{AC}\times \overrightarrow{BC}$

(đã tuân theo thứ tự thì không cần đóng mở ngoặc đơn.)

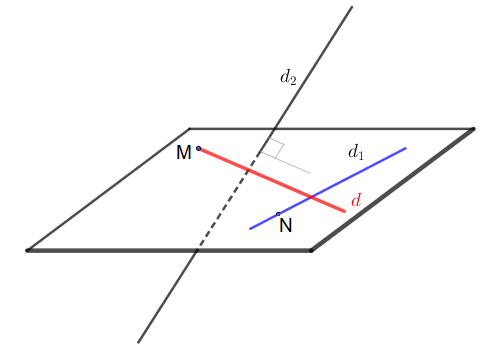
Giả sử $d_1$ đi qua $N$ và vectơ chỉ phương $\overrightarrow{a_1}$, $d_2$ có vectơ chỉ phương $\overrightarrow{a_2}$.

Đường thẳng $d$ cần tìm cắt $d_1$ tạo thành một mặt phẳng, mặt phẳng này có cặp vectơ chỉ phương $\overrightarrow{a_1}, \overrightarrow{MN}$ nên vectơ pháp tuyến là $\overrightarrow{a_1}\times \overrightarrow{MN}$.

Ngoài ra theo đề bài đường thẳng này vuông góc với $d_2$ nên vectơ chỉ phương của nó là
$$\overrightarrow{a_1}\times \overrightarrow{MN}\times \overrightarrow{a_2}$$

 
 
 
 
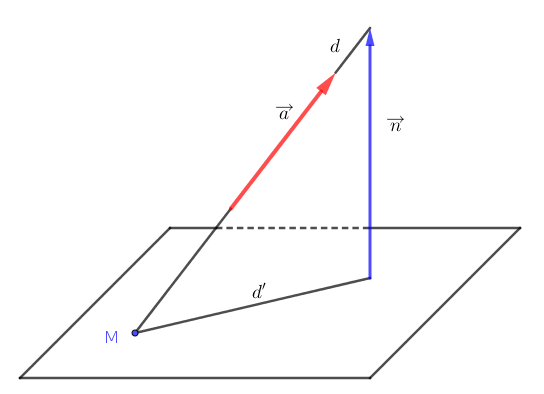
Gọi $d’$ là hình chiếu vuông góc của $d$ trên mặt phẳng $(P)$. Ta thấy $d’$ là giao tuyến của hai mặt phẳng: mặt phẳng $(P)$ và mặt phẳng $(d,d’)$.

Mặt phẳng $(d,d’)$ có cặp vectơ chỉ phương là $\overrightarrow{a}$ và $\overrightarrow{n}$ nên nó có vectơ pháp tuyến là $\overrightarrow{a} \times \overrightarrow{n}$. Ngoài ra $d$ còn vuông góc với $\overrightarrow{n}$ nên vectơ chỉ phương của $d’$ là $$\overrightarrow{a}\times \overrightarrow{n}\times \overrightarrow{n}$$

Xét hai vectơ $\overrightarrow{a}=(1;1;-1), \overrightarrow{n}=(1;2;1)$.

Vectơ $\overrightarrow{u}=\left(\overrightarrow{a}\times \overrightarrow{n}\right) \times \overrightarrow{n}$ là vec tơ chỉ phương của hình chiếu vuông góc.

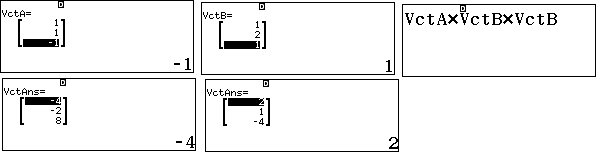
Toạ độ giao điểm của đường thẳng và mặt phẳng là nghiệm của hệ phương trình:

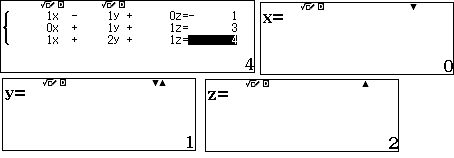
Đối chiếu với 4 phương án

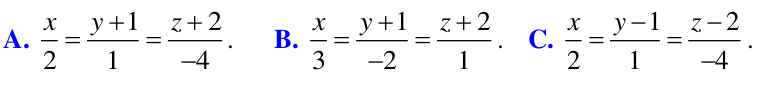
ta chọn C.

About TS. Nguyễn Thái Sơn

nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). Giảng viên thỉnh giảng ĐHSP TP HCM.