Giải câu 49 đề thi TN THPT mã đề 101

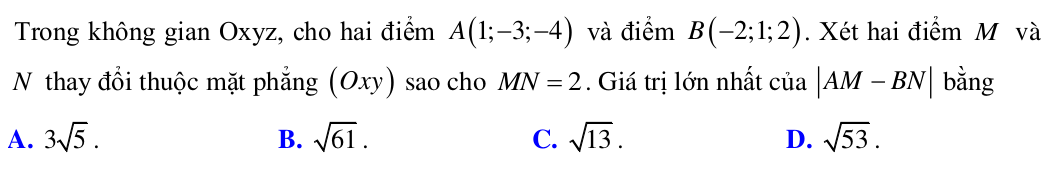
GIẢI

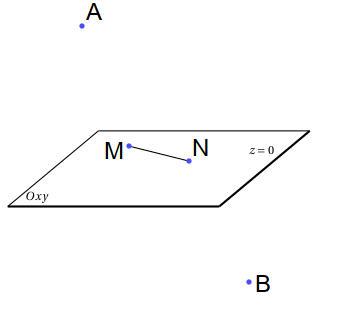
Gợi ý:
 

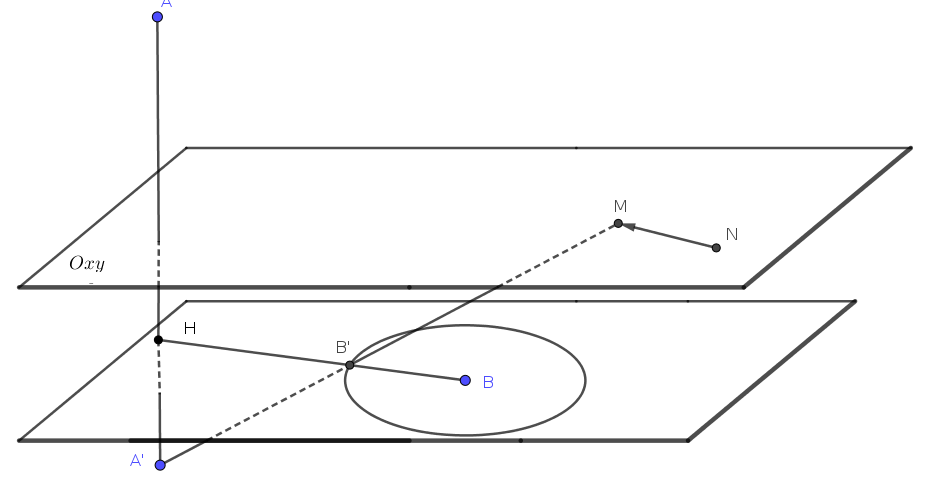
Gọi $A’$ là điểm đối xứng của $A$ qua mặt phẳng $(Oxy)$ và gọi $B’$ là điểm sao cho $\overrightarrow{BB’}=\overrightarrow{NM}$.

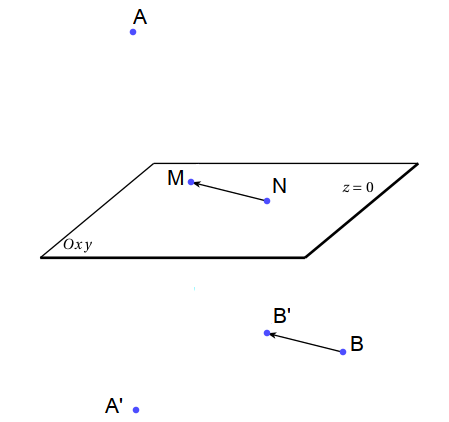
Khi đó $|AM-BN|=|A’M-B’M|\leqslant A’B’.$

Ta thấy $B’$ nằm trên mặt phẳng cố định đi qua $B$ và song song với mặt phẳng $(Oxy)$, mặt phẳng này có phương trình $z=2$ (vì $z_B=2$). Ngoài ra vì $BB’=2$ nên $B’$ chạy trên đường tròn tâm $B$ bán kính 2 vẽ trong mặt phẳng nói trên.

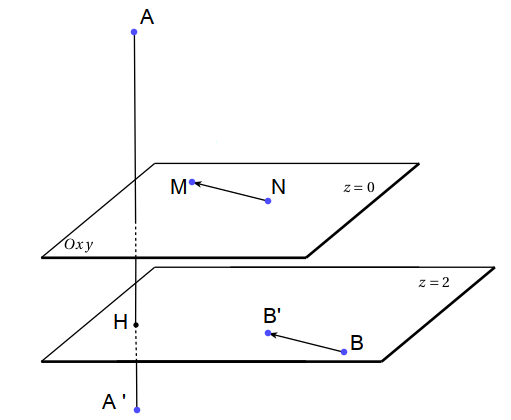
Vì $A(1;-3;-4)$ nên $A'(1;-3;4)$ (do tính chất đối xứng qua mặt phẳng $z=0$) và $H(1;-3;2)$.

$B(-2;1;2)$ nên $HB=5$, $A’H=2$

Ta có $|AM-BN|=|A’M-B’M|\leqslant A’B’=\sqrt{A’H^2+HB’^2} \quad (1)$

Trong đó $A’H=2$ và $HB’\leqslant HB+BB’=5+2=7 \quad (2)$.

Do đó $|AM-BN|\leqslant \sqrt{4+49}=\sqrt{53}.$

Xảy ra dấu “bằng” khi và chỉ khi các bất đẳng thức (1) và (2) xảy ra dấu “bằng”.

(1) xảy ra dấu bằng khi và chỉ khi $M$ nằm trên đường thẳng $A’B’$ và nằm ngoài đoạn $A’B’$.

(2) xảy ra dấu bằng khi và chỉ khi $B’$ nằm trên đoạn $HB$.
 
 
 

Hình vẽ sau đây chỉ ra vị trí chính xác của các điểm $%M$ và $N$ trên mặt phẳng $(Oxy)$ để xảy ra dấu “bằng”.
 

Tóm lại GTLN của $|AM-BN|$ là $\sqrt{53}$.

PS. Dành riêng cho các em đang học 12 (học hè hết chương trình 12 🙂 ):
 
 

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.