BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải câu 41 đề thi minh hoạ 2024
- 22/03/2024
- 251 lượt xem
 |
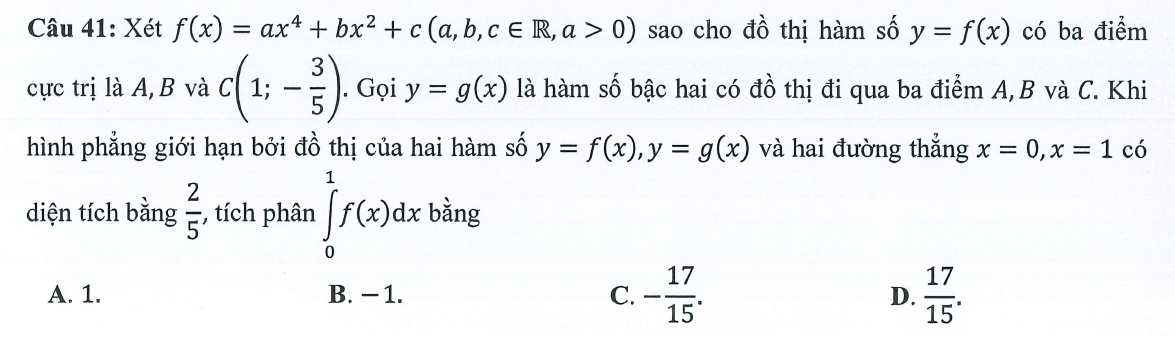Ta có: $f'(x)=4ax^3+2bx$. Vì $x=1$ là một điểm cực trị nên $f'(1)=0 ⇔ 2a+b=0$.
Vì $C\left(1;-\dfrac35\right) \in (C)$ nên $f(1)=-\dfrac35 ⇔ a+b+c=-\dfrac35$.
Ta có $f(x)=f'(x).\dfrac{x}{4} +g(x)⇒ f(x)-g(x)=4ax(x^2-1).\dfrac{x}{4}=ax^2(x^2-1)$
Vì diện tích hình phẳng bằng $\dfrac25$ nên: $$\int_0^1|f(x)-g(x)|dx=\dfrac25 ⇔ \int_0^1a|x^2(x^2-1)|dx=\dfrac25\qquad \text{chú ý}\ a>0 $$.
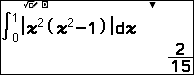. Vậy $a=$ 
lưu vào A.
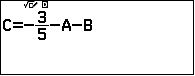
Kết luận: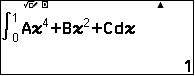 
, ta chọn A.
| Trong bài giải ta sử dụng tính chất sau đây: |
| Nếu hàm số $y=f(x)=ax^4+bx^3+cx^2+dx+e$ có ba điểm cực trị thì khi chia $f(x)$ cho $f'(x)$ ta được thương là $\dfrac{x}{4}+\dfrac{b}{16a}$ và dư là tam thức bậc hai. Đồ thị của hàm số $y$ bằng tam thức bậc hai này chính là parabol đi qua ba điểm cực trị, nghĩa là: $$f(x)=f'(x)\left(\dfrac{x}{4}+\dfrac{b}{16a}\right)+g(x)$$ |
Chia sẻ
About TS. Nguyễn Thái Sơn
