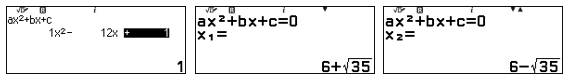BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI BÀI TOÁN NGHIỆM CỦA PHƯƠNG TRÌNH
- 19/03/2024
- 59 lượt xem
Cho \( P(x)=x^{3}+a x^{2}+b x-1 \)
a) Xác đinh số hữu tỉ a và \( b \) để \( x=\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}} \) là nghiêm của \( P(x) \)
b) Với giá trị $a$ và $b$ vừa tìm được tính các nghiêm còn lai của \( P(x) \)
Lời giải
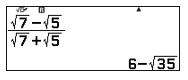
a) Thu gọn giá trị của \( x=\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)
Để \( x=\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}=6-\sqrt{35} \) là nghiệm của \( P(x) \), ta cần tìm giá trị hợp lý của a và b.
Từ phương trình \( P(x)=0 \), ta có:
\((6-\sqrt{35})^{3}+(6-\sqrt{35})^{2} a+(6-\sqrt{35}) b-1=0\)
Rút gọn biểu thức ta được
\(71a+6b+\sqrt{35}(-12a-b)=-845+143\sqrt{35}\)
Đồng nhất vế 2 vế, ta có hệ phương trình:
\(\begin{cases}71a+6b=-845\\-12a-b=143\end{cases}\)
Giải hệ phương trình này, ta tìm được:
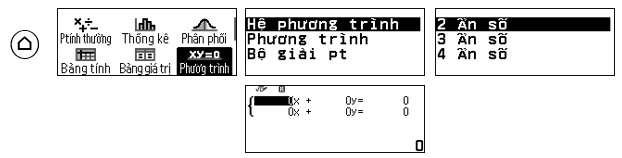
Mở tính năng giải phương trình bậc nhất hai ẩn:
Nhập các hệ số của hệ phương trình \(\begin{cases}71a+6b=-845\\-12a-b=143\end{cases}\)
Vậy \(\begin{cases}a=-13\\b=13\end{cases}\)
Vậy giá trị $a = -13$ và $b = 13$ làm cho \( x=\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}} \) là nghiệm của \( P(x) \).
b) \( P(x)=x^{3}-13 x^{2}+13 x-1 \)
Sử dụng máy tính Fx-880BTG tìm nghiệm của phương trình bậc $3$
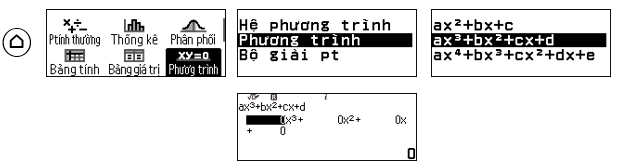
Mở tính năng phương trình bậc 3:
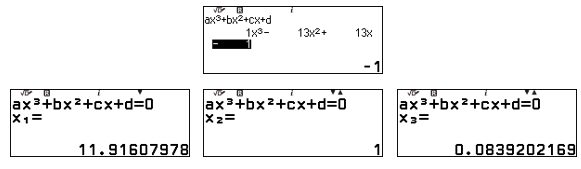
Nhập hệ số của phương trình $P(x)=x^{3}-13 x^{2}+13 x-1=0$
Ta nhận thấy có 1 nghiệm nguyên $x=1$, tiến hành chia đa thức $P(x)$ cho $x-1$
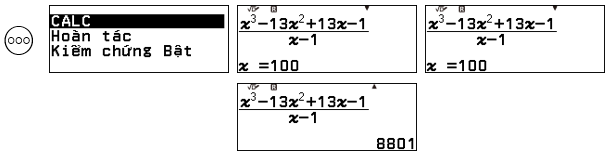
Nhập phương trình $\dfrac{x^3-13x^2+13x-1}{x-1}$
Sử dụng tính năng CALC 100
Phân tích kết quả $8801 \rightarrow 88|01\rightarrow 1|-12|1$
\( P(x)=x^{3}-13 x^{2}+13 x-1=(x-1)(x^2-12x+1)=0 \)
Giải phương trình bậc 2 $x^2-12x+1=0$
Mở tính năng giải phương trình bậc 2:
Nhập các hệ số của phương trình:
Vậy các nghiệm còn lại của phương trình $P(x)=0$ là $1$ và $6+\sqrt{35}$
Chia sẻ
About Toanbitexdtgd1
