BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
CHỨC NĂNG GIẢI PHƯƠNG TRÌNH BẬC 4 TRÊN MÁY CASIO FX 580VNX GIÚP GIẢI NHANH BÀI TOÁN ĐỒ THỊ
- 23/08/2018
- 12,370 lượt xem
Chức năng giải phương trình bậc 4 trên máy tính CASIO fx 580VNX hỗ trợ chúng ta giải toán nhanh hơn so với các phiên bản máy tính trước đó. Bài toán sau minh hoạ cho việc sử dụng chức năng này.
Bài toán minh họa phương trình bậc 4: Đồ thị hàm số $y=f(x)={{x}^{4}}-2{{x}^{2}}-1$ có đồ thị như hình vẽ. Với giá trị nào của $m$ thì phương trình: ${{x}^{4}}-2{{x}^{2}}-4+m=0$ có 4 nghiệm phân biệt?
|
Bài giải tự luận:
Để phương trình $latex {{x}^{4}}-2{{x}^{2}}-4+m=0\Leftrightarrow {{x}^{4}}-2{{x}^{2}}-1=3-m$ có 4 nghiệm phân biệt thì đường thẳng $latex y=3-m$ phải cắt đồ thị hàm số $latex y=f(x)={{x}^{4}}-2{{x}^{2}}-1$ tại 4 điểm phân biệt.
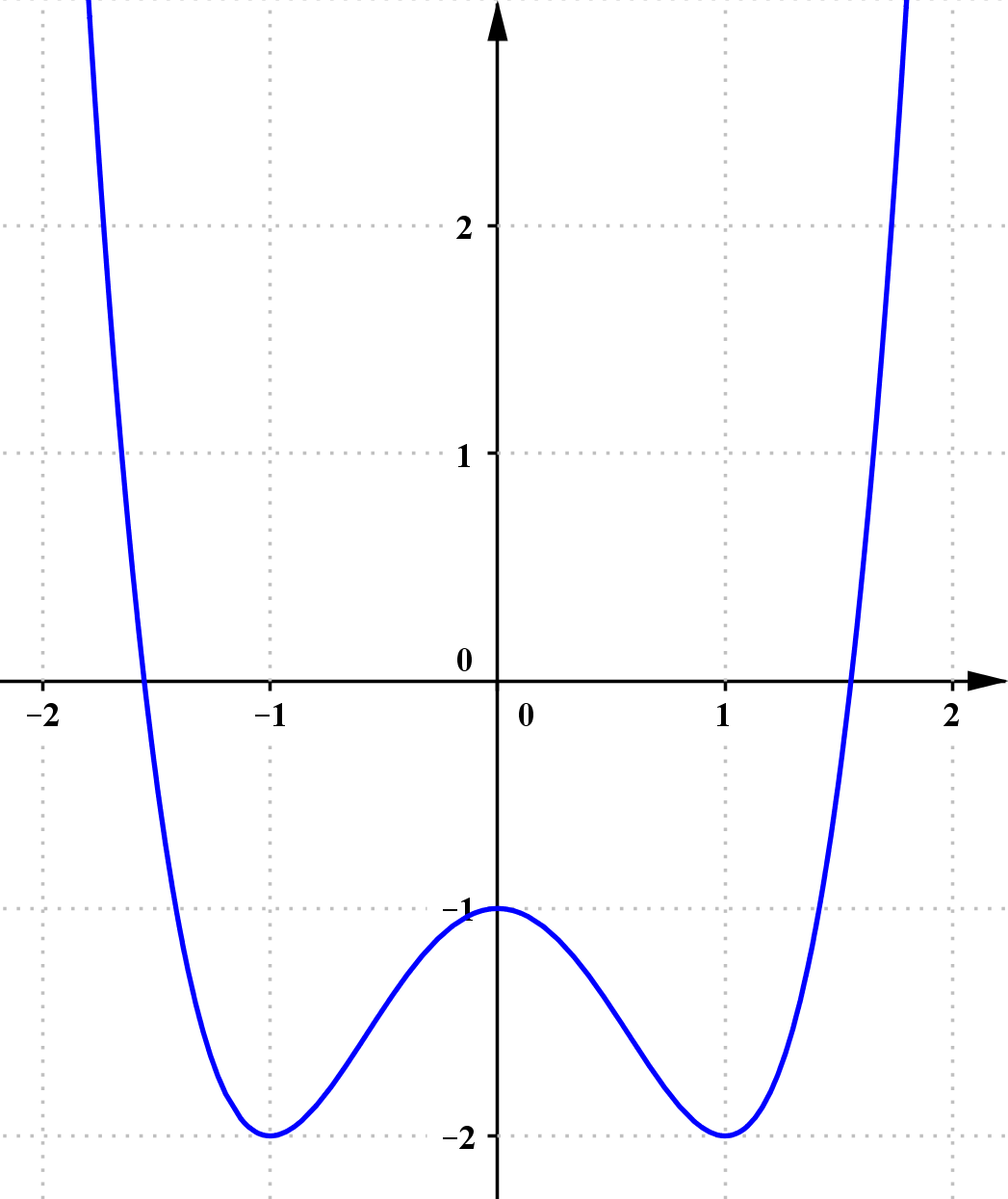
Dựa vào đồ thị ta thấy yêu cầu bài toán tương đương với: $latex -2<3-m<-1\Leftrightarrow 4<m<5$.
Vậy ta chọn đáp án A.
Ta có thể dùng chức năng giải phương trình bậc 4 để kiểm tra một số giá trị của $latex m$, ví dụ ta sẽ kiểm tra lại với $latex m=\dfrac{9}{2}$ (ta chọn giá trị $latex m\in (4;5)$) và với $latex m=4$.
Với $latex m=\dfrac{9}{2}$, phương trình trở thành: $latex {{x}^{4}}-2{{x}^{2}}+\frac{1}{2}=0$
Các bạn thao tác trên máy tính casio fx 580VNX như sau:
Bước 1: Mở chức năng giải phương trình bậc 4
- Cách bấmw924
- Máy tính hiển thị:
Bước 2: Nhập hệ số của phương trình
- Cách bấm: 1=0=p2=1P2==
- Máy tính hiển thị:
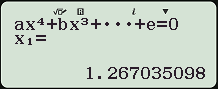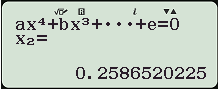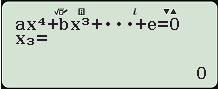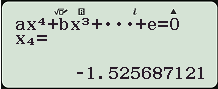
Máy tính hiển thị 4 nghiệm thực phân biệt, nghĩa là $latex m=\dfrac{9}{2}$ thỏa yêu cầu bài toán.
Thao tác tương tự, với $latex m=4$ phương trình trở thành $latex {{x}^{4}}-2{{x}^{2}}=0$
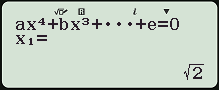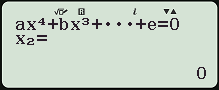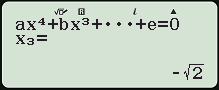
Máy tính hiển thị 3 nghiệm thực phân biệt, nghĩa là $latex m=4$ không thỏa yêu cầu bài toán.
Như vậy chức năng giải phương trình đa thức bậc 4 của máy tính cầm tay CASIO fx 580VNX giúp chúng ta nhanh chóng kiểm tra kết quả của bài toán.
Các bạn có thể xem thêm về các tính năng nổi trội của máy tính cầm tay CASIO fx 580VNX tại đây.
About TailieuCasio
