BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Dùng bảng tính xây dựng dãy số quy nạp
- 30/10/2023
- 545 lượt xem
|
Để chuẩn bị tốt cho kỳ thi HSG MTCT cấp tỉnh (thành phố) chúng ta ôn lại cách xử lý dãy số quy nạp trên MT CASIO fx-880BTG |
Bài toán kỳ này:
Nhận xét rằng biểu thức quy nạp nói trên có thể viết lại dưới dạng một biểu thức như sau:
$$u_{n+2}=\dfrac{1-(-1)^{n+2}}{2}(3u_{n+1}-2u_n)+\dfrac{1-(-1)^{n+1}}{2}(2u_{n+1}+3u_n-1)$$ với $n \geqslant 1$. Nghĩa là:
$u_3=1.(3u_2-2u_1)+0.(2u_2+3u_1-1)$
$u_4=0.(3u_3-2u_2)+1.(2u_3+3u_2-1)$
v.v…
Ta thao tác trên trên MÁY TÍNH Casio fx-880BTG như sau:
1. Mở một bảng tính, đánh số tử 1 đến 21 vào cột A. Điền công thức $(1-(-1)^{A_1})/2$ vào B1:B21
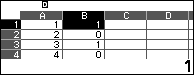
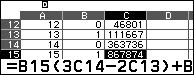
2. Đưa con trỏ vào C1 nhập 1, xuống C2 nhập 2 và xuống C3 điền công thức:
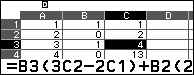
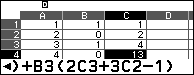
Ở hình trên $B2=0$ nên đó là công thức tính C3=3C2-2C1,
ở hình dưới $B4=0$ nên đó là công thức tính C4=2C3+3C2-1.
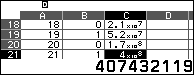
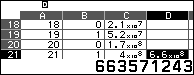
3. Đưa con trỏ vào C10, C15, C21 ta có kết quả:
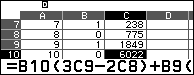
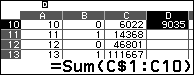
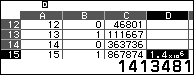
4. Đưa con trỏ tới D10, nhập công thức Sum(C$\$$1:C10) (chú ý có dấu $\$$), sau đó copy và dán công thức này sang D15, D21
About TS. Nguyễn Thái Sơn
