Dùng bảng tính để tính tứ phân vị của mẫu số liệu ghép nhóm.
- 15/11/2023
- 928 lượt xem
|
Cho mẫu số liệu ghép nhóm
$a_1, a_2, a_3, a_4, \dots , a_{n}, a_{n+1}$ trên mỗi đoạn $[a_i,a_{i+1}]$ số liệu có tần số là $n_i\ (i=1,2,3\dots, n)$. Ta tính tứ phân vị của mẫu số liệu ghép nhóm nói trên. |
Sau đây là các công thức để tính tứ phân vị:
$$Q_k=a_m+\displaystyle \left(\dfrac{k}{4}.n-c_{m-1}\right).\dfrac{a_{m+1}-a_m}{n_m} \qquad (k=1,2,3).$$
ký hiệu $\displaystyle n=\sum_{i=1}^{n}n_i, c_{m-1}=\sum_{i=1}^{m-1}n_i$.
trong các công thức 2 và 3, $m$ được chọn sao cho: nhóm $[a_m;a_{m+1})$ chứa các tứ phân vị.
|
BÀI TẬP
Cho mẫu số liệu ghép nhóm $0, 10, 20, 30, 40, 50, 60, 70, 80$ trên mỗi đoạn tương ứng số liệu có tần số là $5, 24, 13, 12, 20, 11, 12, 30$. Ta tính trung bình, mod và tứ phân vị của mẫu số liệu ghép nhóm nói trên theo từng bước. |
- Bước 1: Mở một bảng tính, cột A nhập liệu, cột B nhập tần số tương ứng (lưu ý cột B ít hơn một dòng so với cột A).
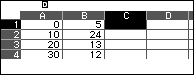
- Bước 2: Tính tần số tích luỹ $\displaystyle c_m=\sum_{i=1}^{m}n_i\quad (m=1,2,3\dots, n)$, đặt $c_n=n$.
Đưa con trỏ vào C1, điền công thức Sum(B$\$$1:B1). B1 thứ nhất là cố định vị trí đầu (khi tính tổng) nên có dấu $\$$, B1 thứ hai dùng để copy xuống theo phạm vi từ C1 đến C8 thành B2, B3, …, B8.
Kết quả

Ta thấy cỡ mẫu là 127.
- Bước 3: Tính trung vị $M_e=Q_2$.
Đưa con trỏ qua cột D, lấy cỡ mẫu chia 2 trừ cho tần số tích luỹ từ thấp lên cao, khi gặp số âm đầu tiên thì dừng lại, tại đó là trung vị.
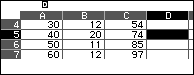
Đứng tại đây nhập công thức tính $Q_2$.
$$Q_2=A_5+\left(0.5C\$8-C4\right).\dfrac{A_6-A_5}{B_5}$$ 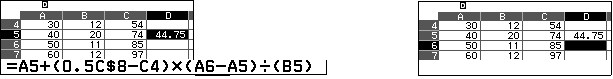
- Bước 4: Tính tứ phân vị $Q_1$.
Để con trỏ tại trung vị ($C_5$), ra lệnh

Lấy cỡ mẫu chia 4 trừ cho tần số tích luỹ từ thấp lên cao, khi gặp số âm đầu tiên thì dừng lại, tại đó là $Q_1$.
Đưa con trỏ vào vị trí $Q_1$, nhấn OK để dán, sau đó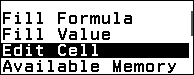 để điều chỉnh số $0,5$ thành $0,25$ ứng với công thức:
để điều chỉnh số $0,5$ thành $0,25$ ứng với công thức: $$Q_1=A_3+\left(0.25C\$8-C2\right).\dfrac{A_4-A_3}{B_3}$$ 
- Bước 5: Tính tứ phân vị $Q_3$.
Để con trỏ tại trung vị ($C_5$), ra lệnh

Lấy cỡ mẫu nhân cho $\dfrac34$ trừ cho tần số tích luỹ từ thấp lên cao, khi gặp số âm đầu tiên thì dừng lại, tại đó là $Q_3$.
Đưa con trỏ vào vị trí $Q_3$, nhấn OK để dán, sau đó để điều chỉnh số $0,5$ thành $0,75$ ứng với công thức:
để điều chỉnh số $0,5$ thành $0,75$ ứng với công thức: $$Q_3=A_7+\left(0.75C\$8-C6\right).\dfrac{A_8-A_7}{B_7}$$ 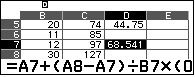
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay