MỘT SỐ BÀI TOÁN VỀ NHỊ THỨC NEWTON TRONG ĐỀ THI HSG MÁY TÍNH CẦM TAY- PHẦN 2
- 29/03/2022
- 946 lượt xem
Bài 4. Tính gần đúng \[A={{10}^{6}}\left( \dfrac{1}{3}C_{2015}^{0}-\dfrac{1}{5}C_{2015}^{1}+\dfrac{1}{7}C_{2015}^{2}-\dfrac{1}{9}C_{2015}^{3}+…-\dfrac{1}{4033}C_{2015}^{2015} \right)\].
Hướng dẫn giải
Ta có \[{{\left( 1-{{x}^{2}} \right)}^{2015}}=C_{2015}^{0}-C_{2015}^{1}{{x}^{2}}+C_{2015}^{2}{{x}^{4}}-…-C_{2015}^{2015}{{x}^{4030}}\]
Suy ra \[{{x}^{2}}{{\left( 1-{{x}^{2}} \right)}^{2015}}=C_{2015}^{0}{{x}^{2}}-C_{2015}^{1}{{x}^{4}}+C_{2015}^{2}{{x}^{6}}-…-C_{2015}^{2015}{{x}^{4032}}\]
Do đó \[\int\limits_{0}^{1}{{{x}^{2}}{{\left( 1-{{x}^{2}} \right)}^{2015}}dx}=\int\limits_{0}^{1}{\left( C_{2015}^{0}{{x}^{2}}-C_{2015}^{1}{{x}^{4}}+C_{2015}^{2}{{x}^{6}}-…-C_{2015}^{2015}{{x}^{4032}} \right)}dx\]
Suy ra \[A={{10}^{6}}.\int\limits_{0}^{1}{{{x}^{2}}{{\left( 1-{{x}^{2}} \right)}^{2015}}dx}\approx 4,894388\]
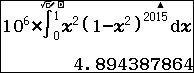
Bài 5. Khai triển
${{\left( 1+x+{{x}^{2}}+…+{{x}^{2015}} \right)}^{3}}$ thành ${{A}_{0}}+{{A}_{1}}x+…+{{A}_{2015}}{{x}^{2015}}+…+{{A}_{6045}}{{x}^{6045}}$
Tính hệ số ${{A}_{2015}}$ của ${{x}^{2015}}$.
Hướng dẫn giải
Khi khai triển ${{\left( 1+x+{{x}^{2}}+…+{{x}^{2015}} \right)}^{3}}$ , số hạng chứa ${{x}^{2015}}$ là:
${{x}^{0}}{{x}^{0}}{{x}^{2015}}+{{x}^{0}}{{x}^{2015}}{{x}^{0}}+{{x}^{2015}}{{x}^{0}}{{x}^{0}}+{{x}^{0}}{{x}^{1}}{{x}^{2014}}+{{x}^{0}}{{x}^{2014}}{{x}^{1}}+{{x}^{1}}{{x}^{0}}{{x}^{2014}}+{{x}^{1}}{{x}^{2014}}{{x}^{0}}+{{x}^{2014}}{{x}^{0}}{{x}^{1}}+{{x}^{2014}}{{x}^{1}}{{x}^{0}}+…$
Mỗi thành phần trong số hạng chứa ${{x}^{2015}}$ có hệ số bằng 1 và có dạng ${{x}^{m}}.{{x}^{n}}.{{x}^{k}}$, trong đó:
$$\left\{ \begin{align} & m,n,k\in \left\{ 0;1;2;3;…;2015 \right\} \\ & m+n+k=2015 \\ \end{align} \right.$$
Cần tìm số các bộ số $\left( m;n;k \right)$ thỏa mãn điều kiện trên, đó cũng là hệ số của ${{x}^{2015}}$.
Ta chia làm các trường hợp sau:
+ Trường hợp 1: Nếu $m=0$ thì $(n;k)$ thỏa mãn bài toán này là: $(0;2015),(1;2014),(2;2013),…,(2015;0)$, suy ra có 2016 bộ số $\left( m;n;k \right)$.
+ Trường hợp 2: Nếu $m=1$ thì $(n;k)$ thỏa mãn bài toán này là: $(0;2014),(1;2013),(2;2012),…,(2014;0)$, suy ra có 2015 bộ số $\left( m;n;k \right)$.
+ Trường hợp 3: Nếu $m=2$ thì $(n;k)$ thỏa mãn bài toán này là: $(0;2013),(1;2012),(2;2011),…,(2013;0)$, suy ra có 2016 bộ số $\left( m;n;k \right)$.
…
+ Trường hợp 2015: Nếu $m=0$ thì $(n;k)$ thỏa mãn bài toán này là:
$(0;0)$ , suy ra có 1 bộ số $\left( m;n;k \right)$.
Vậy có: $1+2+3+…+2016=\dfrac{2016\times 2017}{2}=2.033.136$
Bộ số $\left( m;n;k \right)$thỏa mãn yêu cầu bài toán. Suy ra ${{A}_{2015}}=2.033.136$
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay