BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
TÍNH TÍCH VÔ HƯỚNG CÓ HƯỚNG VÉC TƠ
- 24/03/2022
- 455 lượt xem
Phương pháp
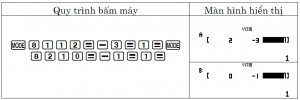
$\lozenge$ Lệnh đăng nhập môi trường véc tơ MODE 8
$\lozenge$ Nhập thông số véc tơ MODE 8 1 1
$\lozenge$ Tính tích vô hướng hai véc tơ: vecto A shift 5 7 vecto B
$\lozenge$ Tính tích có hướng hai véc tơ: vecto A vecto B
$\lozenge$ Lệnh giá trị tuyệt đối SHIFT HYP
$\bullet$ Chức năng 
(VECTOR)
Khi đó màn hình máy tính xuất hiện như sau:
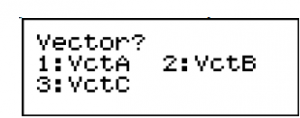
Nhập dữ liệu cho từng vectơ: Chọn 
để nhập cho Vectơ A.
Chọn để chọn hệ trục tọa độ Oxyz
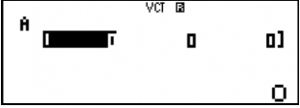
Ví dụ: $\vec{a}=(1;2;3), \vec{b}=(3;2;1), \vec{c}=(4;5;6)$
Nhập $\vec{a}=(1;2;3)$ thì bấm 
.
Để nhập tiếp dữ liệu cho vectơ B thì bấm
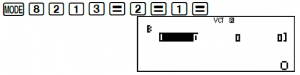
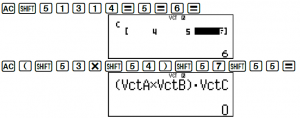
Tính tích có hướng hai vectơ A và B bấm như sau
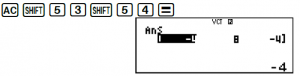
Tính tích vô hướng của hai vectơ A và B bấm như sau
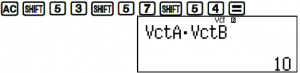
Để tính hỗn tạp 3 vectơ thì sẽ nhập thêm dữ liệu cho vectơ C
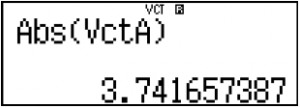
Để tính độ dài vectơ A, bấm 
Ví dụ 1: Trong không gian với hệ tọa độ $Oxyz$ cho $A(1;2;0), B(3;-1;1), C(1;1;1)$. Tính diện tích $S$ của tam giác $ABC$.
| A. $S=\sqrt{3}$ | B. $S=\sqrt{2}$ | C. $\dfrac{1}{2}$ | D. $S=1$ |
Lời giải
Nhập hai vectơ $\overrightarrow{AB}, \overrightarrow{AC}$ vào máy tính Casio
Diện tích tam giác $ABC$ là : $S_{ABC}=\dfrac{1}{2}\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC}\right]\right\vert$
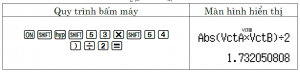
Chọn A.
Ví dụ 2: Cho $A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1)$. Thể tích tứ diện $ABCD$ bằng
| A. $30$ | B. $40$ | C. $50$ | D. $60$ |
Lời giải
Thể tích tứ diện $ABCD$: $V=\dfrac{1}{6}\left\vert \overrightarrow{AB}\left[\overrightarrow{AC};\overrightarrow{AD}\right]\right\vert $
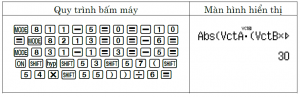
Do đó, $V=\dfrac{1}{6}\left\vert \overrightarrow{AB}\left[\overrightarrow{AC};\overrightarrow{AD}\right]\right\vert =30$. Chọn A
Ví dụ 3: Tính góc giữa đường thẳng $\Delta: \dfrac{x+3}{2}=\dfrac{y+1}{1}=\dfrac{z-3}{1}$ và mặt phẳng $(P): x+2y-z+5=0$
| A. $30^o$ | B. $45^o$ | C. $60^o$ | D. $90^o$ |
Lời giải
Đường thẳng $\Delta$ có vectơ chỉ phương $\vec{u}(2;1;1)$ và mặt phẳng $(P)$ có vectơ pháp tuyến $\vec{n}(1;2;-1)$.
Gọi $\beta$ là góc giữa hai vectơ $\vec{u}$ và $\vec{n}$. Ta có $\sin\left(\widehat{\Delta,(P)}\right)=\left\vert\cos\beta\right\vert=\dfrac{\left\vert \vec{u}.\vec{n}\right\vert}{\left\vert\vec{u}\right\vert.\left\vert\vec{n}\right\vert}$
Gọi $\alpha$ là góc giữa đường thẳng $\Delta$ và mặt phẳng $(P)$. Ta có $\sin\alpha= \vert\cos \beta\vert=0.5$ $\Rightarrow$ $\alpha=30^o$. Chọn A.
Ví dụ 4: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d: \dfrac{x-1}{1}=\dfrac{y-2}{2}= \dfrac{z+2}{-2}$. Tính khoảng cách từ điểm $M(-2;1;-1)$ tới $d$
| A. $\dfrac{5}{3}$ | B. $\dfrac{5\sqrt{2}}{2}$ | C. $\dfrac{\sqrt{2}}{3}$ | D. $\dfrac{5\sqrt{2}}{3}$ |
Lời giải
Khoảng cách từ $M$ tới $d$ tính theo công thức: $d(M; d)= \dfrac{\left\vert \left[ \overrightarrow{MN},\overrightarrow{u}\right]\right\vert }{\vert\overrightarrow{u}\vert}$.
Nhập hai vectơ $MN, u_d$ vào máy tính.
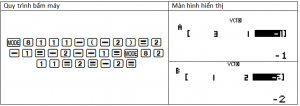
Tính $d(M; d)= \dfrac{\left\vert \left[ \overrightarrow{MN},\overrightarrow{u}\right]\right\vert }{\vert\overrightarrow{u}\vert}$.
Chọn D.
Ví dụ 5: Tính khoảng cách giữa hai đường thẳng:
$d: \dfrac{x-1}{1}=\dfrac{y+2}{1}=\dfrac{z-3}{-1}$ và $d’$:$\begin{cases} x&=t\\ y&=1+2t\qquad (t\in \mathbb{R})\\ z&=6+3t\end{cases}$
| A. $\dfrac{\sqrt{42}}{9}$ | B. $\dfrac{\sqrt{46}}{9}$ | C. $\dfrac{\sqrt{46}}{3}$ | D. $\dfrac{\sqrt{42}}{3}$ |
Lời giải
$M(1;-2;3)\in d$ và $d$ có vecto chỉ phương $\vec{u_d}(1;1,-1)$.
$M'(0;1;6)\in d’$ và $d’$ có vecto chỉ phương $\vec{u_{d’}}(1;2;3)$.
Ta có $\overrightarrow{MM’}(-1;3;3)$. Hai đường thẳng trên chéo nhau.
Khoảng cách hai đường thẳng là $d(d;d’)= \dfrac{\left\vert\overrightarrow{MM’}\left[ \vec{u_d},\vec{u_{d’}}\right] \right\vert}{\left\vert\left[ \vec{u_d},\vec{u_{d’}}\right]\right\vert}$.
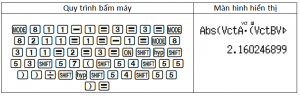
Chọn D.
About Tạ Quang Tuấn
