BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
KĨ THUẬT GIẢI NHANH BÀI TOÁN TÌM GTLN-GTNN CỦA HÀM SỐ TRÊN ĐOẠN [a;b].
- 24/03/2022
- 464 lượt xem
SỬ DỤNG TÍNH NĂNG BẢNG GIÁ TRỊ TABLE
Phương pháp:
$\lozenge$ Nhấn 
$\lozenge$ $f(x)=$ nhập hàm số vào.
$\lozenge$ Step? Nhập giá trị $a$.
$\lozenge$ End? Nhập giá trị $b$.
$\lozenge$ Step? Nhập giá trị: $0,1; 0,2; 0,5$ và $1$ tùy vào đoạn $[a;b]$.
Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.
$\blacksquare$ Chú ý:
– Ta thiết lập miền giá trị của biến $x$ Start $a$ End $b$ Step ( có thể làm tròn để Step đẹp).
– Hàm số chứa $\sin x, \cos x$, tan\,$x$ ta chuyển máy tính về chế độ Radian: 
Ví dụ 1: Giá trị nhỏ nhất của hàm số $y=\dfrac{x^2+3}{x-1}$ trên đoạn $[2;4]$ là
| A. $6 $ | B. $-2 $ | C.$-3$ | D.$\dfrac{19}{3}$ |
Lời giải
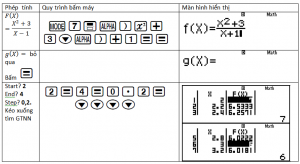
Quan sát bảng giá trị tìm kết quả nào gần đáp án để kết luận.
$ \Longrightarrow$ Chọn A.
SỬ DỤNG TÍNH NĂNG SOLVE
Phương pháp:
$\lozenge$ Để tìm giá trị lớn nhất (GTLN) $M$, giá trị nhỏ nhất (GTNN) $m$ của hàm số $y=f(x)$ ta giải phương trình $ f(x)-M=0, f(x)-m=0$.
$\lozenge$ Tìm GTLN ta thay các đáp án từ lớn đến nhỏ sau đó sử dụng SOLVE để tìm nghiệm, nếu nghiệm thuộc đoạn, khoảng đã cho ta chọn luôn.
$\lozenge$ Tìm GTNN ta thay đáp án từ nhỏ đến lớn.
Ví dụ 2: Tìm giá trị lớn nhất của hàm số $y= x^3-2x^2 -4x+1$ trên đoạn $[1;3]$
| A. $\max=\dfrac{67}{27}$ | B. $\max=-2$ | C. $\max=-7$ | D. $\max=-4$ |
Lời giải
Các kết quả xếp theo thứ tự $ \dfrac{67}{27}> -2>-4>-7$. Do vậy ta giải phương trình $x^3-2x^2 -4x+1=\dfrac{67}{27}$ trước
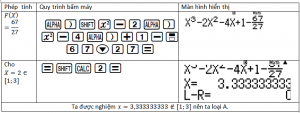
+ Tiếp theo ta thay đáp án $\max=-2$, giải phương trình:
$$x^3-2x^2-4x+1=-2$$
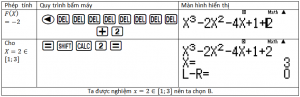
Không thử các đáp án còn lại nữa vì $F(X)=-2$ đã là lớn nhất.
$\blacksquare$ Chú ý: Kĩ thuật SOLVE tuy tiến hành lâu hơn nhưng mạnh hơn, đảm bảo chắc chắn hơn TABLE nhiều đặc biệt với các bạn còn thiếu kĩ năng phân tích bảng giá trị.
About Tạ Quang Tuấn
