BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Vận dụng công thức góc giữa hai mặt bên của khối tứ diện
- 01/06/2022
- 317 lượt xem
Hướng dẫn:
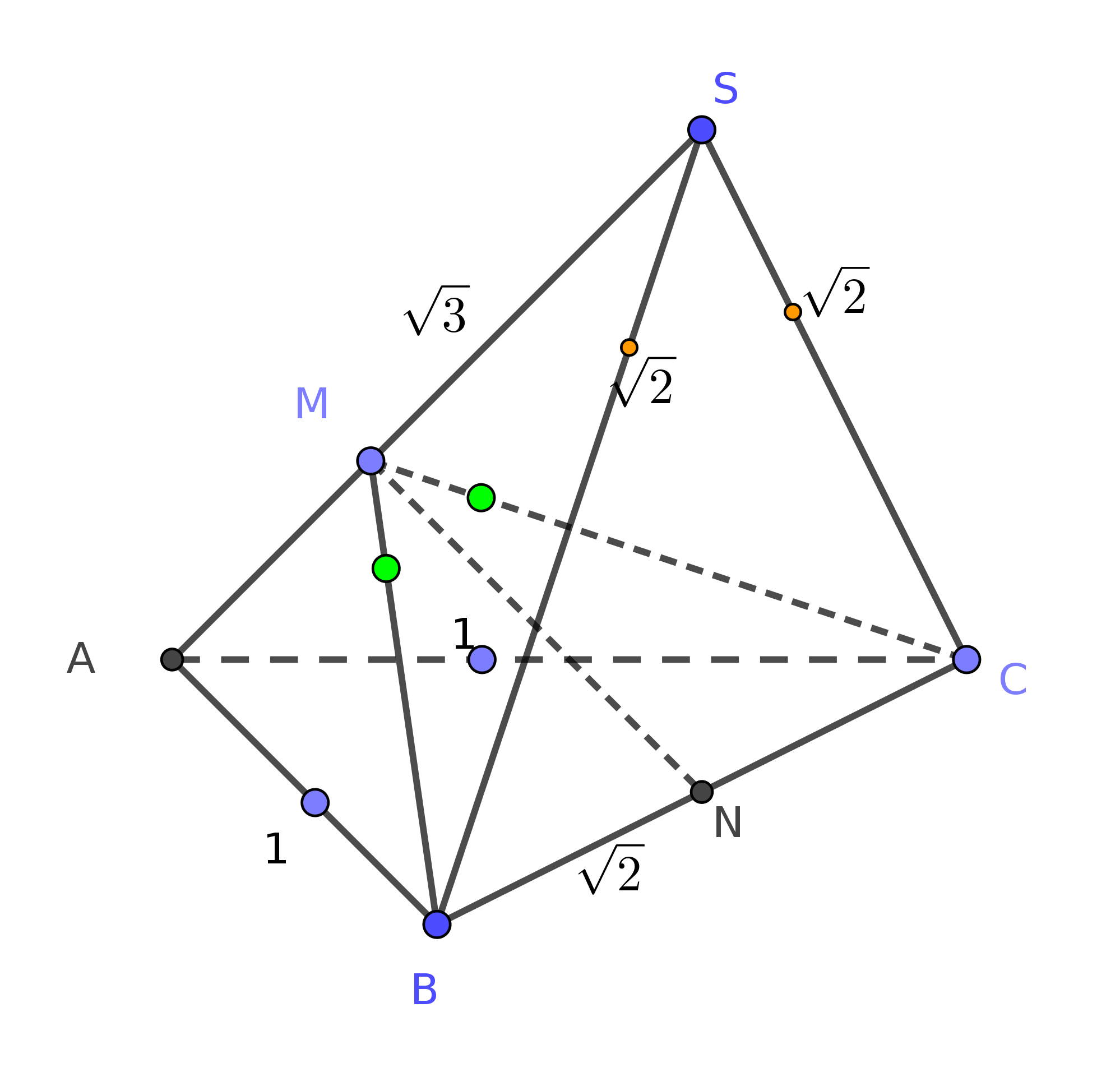
Gọi $N$ là trung điểm $BC$.
Nhận xét rằng vì $AB=AC$ và $SB=SC$ nên $BC\perp SA$ do đó hạ $BM\perp SA$ thì góc $\widehat{BMC}=120^\circ$.
Suy ra $\widehat{BMN}=60^\circ$.
Dựa vào các hệ thức lượng trong tam giác vuông $BMN$ và $SAB$ ta tính được $SB=SC=a\sqrt2$ và $SA=a\sqrt3$.
Theo công thức góc tạo bởi hai mặt bên của Khối tứ diện ta có:
| $$\sin 120^\circ =\dfrac32.\dfrac{V_{SABC}.SA}{S_{SAB}.S_{ABC}}$$ |
Vậy
| $$V_{SABC} =\dfrac23.\dfrac{S_{SAB}.S_{ABC}.\sin 120^\circ}{SA}=\dfrac16\dfrac{AB^2.SB^2.\sin 120^\circ}{SA}$$ |
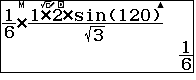
Ta chọn D.
Chia sẻ
About TS. Nguyễn Thái Sơn
