BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
TÌM NHANH CỰC TRỊ HÀM SỐ BẬC 3 TRÊN CASIO FX 580VNX
- 22/08/2018
- 7,790 lượt xem
Máy tính CASIO fx 580VNX có một tính năng mới đặc biệt hữu dụng với các bạn học sinh là tìm điểm cực trị hàm số bậc 3. Ta cùng tìm hiểu tính năng này qua bài toán sau:
Tìm nhanh cực trị hàm số bậc 3: Cho cực trị hàm số $latex f(x)=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}-x+m+1$. Tìm tất cả các giá trị của $latex m$ để hàm số có hai điểm cực trị $latex A({{x}_{A}},{{y}_{A}})$ và $latex B({{x}_{B}},{{y}_{B}})$ thỏa mãn: $latex x_{A}^{2}+x_{B}^{2}=2$.
|
Bài giải tự luận tìm cực trị hàm số bậc 3:
Ta có $latex f'(x)={{x}^{2}}-2mx-1$, vì $ac=1.(-1)<0$ nên phương trình $latex f'(x)=0$ luôn có 2 nghiệm phân biệt. Do đó ta có:
$latex x_A^2 + x_B^2 = 2 \Leftrightarrow {\left( {{x_A} + {x_B}} \right)^2} – 2{x_A}{x_B} = 2{\rm{ (1)}}$
Áp dụng hệ thức Vi-et ta có: $latex \left\{ \begin{align} & {{x}_{A}}+{{x}_{B}}=2m \\ & {{x}_{A}}{{x}_{B}}=-1 \\ \end{align} \right.$, thay vào biểu thức (1) ta được:
$latex {\left( {2m} \right)^2} – 2.( – 1) = 2 \Leftrightarrow m = 0$
Vậy ta chọn đáp án A.
Ta có thể kiểm tra lại kết quả như sau:
Bước 1: Chọn chức năng giải phương trình hàm số bậc 3 trên casio fx 580vnx :
- Cách bấm: w923
- Máy tính hiển thị:
Bước 2: Với $latex m = 0$, ta có $latex f(x) = \frac{1}{3}{x^3} – x + 1$ . Ta nhập các hệ số vào máy tính:
- Cách bấm máy tính: 1P3=0=p1=1=
- Máy tính hiển thị:
Bước 3: Nhấn phím = cho đến khi máy tính hiển thị các giá trị cực trị hàm số, ta lần lượt lưu các giá trị đó vào $latex A$ và $latex B$.
- Cách bấm: C====Jz==Jx
- Máy tính hiển thị:
Bước 4: Thực hiện phép tính $latex {{A}^{2}}+{{B}^{2}}$
- Cách bấm máy tính: w1Qzd+Qxd=
- Máy tính hiển thị:
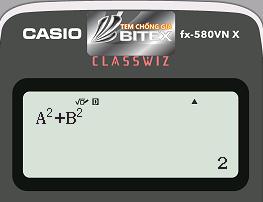
Cách tìm cực trị hàm số bậc 3 trên casio fx 580vn x
Ta thấy kết quả vừa hiển thị chính xác với yêu cầu bài toán, do đó $latex m=0$ là đáp án đúng.
Chức năng tìm cực trị hàm bậc 3 hỗ trợ rất hiệu quả trong việc giải nhanh toán bằng máy tính casio fx 580vnx. Trong các bài viết tiếp theo diendanmaytinhcamtay.vn sẽ khai thác chức năng này nhiều hơn.
About TailieuCasio
