Phép giải tam giác thường với một chiều cao cho trước
- 04/01/2024
- 101 lượt xem
2021. Cho tam giác ABC có AB = 4,7, trung tuyến AM = 5, 4 và đường cao BH = 3,7. Gọi O là giao điểm của AM và BH. Tính gần đúng (chính xác đến 2 chữ số thập phân)
|
| ĐS: $AC\approx 7,25; BC\approx 5,71; OA\approx 3.08; S\approx 2,87; r\approx 0,74$ |
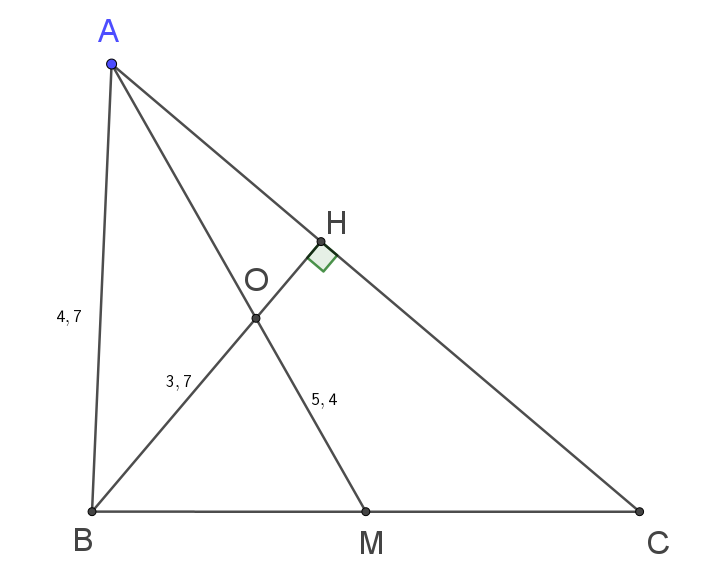
a) Để tính $AC$ và $BC$ ta dùng hai hệ thức:
$AB^2+AC^2=2AM^2+\dfrac{BC^2}{2}\qquad (1)$
$BC^2=AB^2+AC^2-2AB.AC.\cos A\qquad (2)$
trong đó $\widehat{A}=$  lưu vào biến A.
lưu vào biến A.
Thay (2) vào (1) ta có phương trình:
$$AB^2+x^2=2AM^2+\dfrac12(AB^2+x^2-2AB.x.\cos A)\qquad (3) $$
Đây là phương trình bậc hai có một nghiệm âm (loại) và một nghiệm dương cần tìm.
Nhập nguyên si (hoặc thu gọn) phương trình (3) lên máy tính với phương thức Solver (Bộ giải phương trình) của máy tính Casio fx-880BTG ta có nghiệm 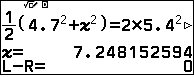
lưu nghiệm này vào B.
Thay $AC$ tìm được vào (2) ta tính được $BC$: 
lưu nghiệm vào C.
Tính $AH=$  lưu vào D.
lưu vào D.
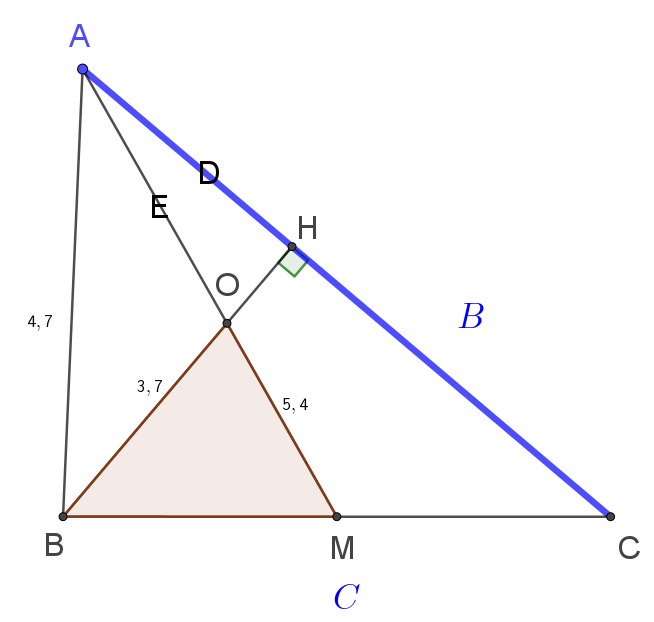
Để tính $AO$ ta áp dụng định lý Me-nê-la-uyt vào tam giác $OMB$ với cát tuyến AHC:
$$\dfrac{AO}{AM}.\dfrac{CM}{CB}.\dfrac{HB}{HO}=1$$
Đặt $AO=x \Rightarrow HO=\sqrt{x^2-AH^2}$
Dùng Solver với giá trị nhập vào là 3:
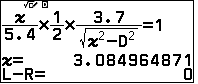
lưu nghiệm vào E.
b) Diện tích tam giác $BOM$ bằng:
$$S=\dfrac12.OB.OM.\sin\widehat{BOM}=\dfrac12.(BH-OH).(AM-AO).\dfrac{AH}{AO}$$
Chú ý: $\widehat{BOM}=\widehat{AOM}$.
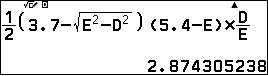
lưu diện tích vào F.
c) Bán kính đường tròn nội tiếp tam giác cho bởi công thức: $r=\dfrac{S}{p}$, trong đó $p$ là nửa chu vi.
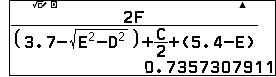
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay