BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Phép giải tam giác thường khi biết ba cạnh.
- 06/01/2024
- 110 lượt xem
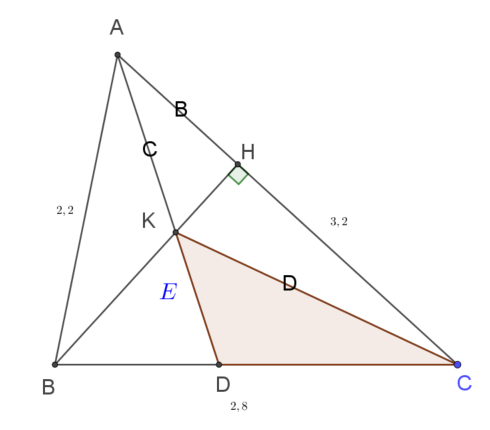
| 2023. Cho tam giác ABC có AB = 2,2cm, AC = 3,2 cm, BC = 2,8 cm. Đường cao BH và phân giác trong AD của tam giác ABC cắt nhau tại K. Tính gần đúng (chính xác đến 2 chữ số thập phân sau dấu phẩy):
a) Độ dài các đoạn thẳng AK, CK. |
| Đáp án: $AK ≈ \ 1,30 cm; CK ≈ \ 2,17 cm, S_{CKD}≈ 0,76\ cm^2; R_{BKD}≈ R. 0,66\ cm$ |
a) $\widehat{A}=\cos^{-1}\dfrac{AB^2+AC^2-BC^2}{2AB.AC}$ 
lưu vào A.
Suy ra $AH=$ 
lưu vào B.
Vậy $AK=$ 
$CK=\sqrt{AK^2+AC^2-2AK.AC.\cos\dfrac{A}{2}}$ 
b) Độ dài đường phân giác $AD=\dfrac{2AB.AC.\cos\dfrac{A}{2}}{AB+AC}$ 
lưu vào E.
$S_{CDK}=S_{CDA}-S_{CKA}=\dfrac12AD.AC\sin\dfrac{A}{2}-\dfrac12AK.AC.\sin\dfrac{A}{2}$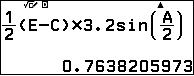 
c) Bán kính đường tròn ngoại tiếp tam giác BKD ta áp dụng công thức:
$R=\dfrac{KD}{2\sin\widehat{KBD}}=\dfrac{AD-AK}{2.\dfrac{HC}{BC}}$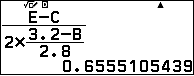 
| PS. Để giải tam thường học sinh buộc phải biết một số hệ thức lượng trong tam giác. Các hệ thức lượng này có thể chứng minh được với kiến thức lớp 9. |
Chia sẻ
About TS. Nguyễn Thái Sơn
