Phép giải tam giác khi biết một chiều cao (bài 2)
- 06/01/2024
- 127 lượt xem
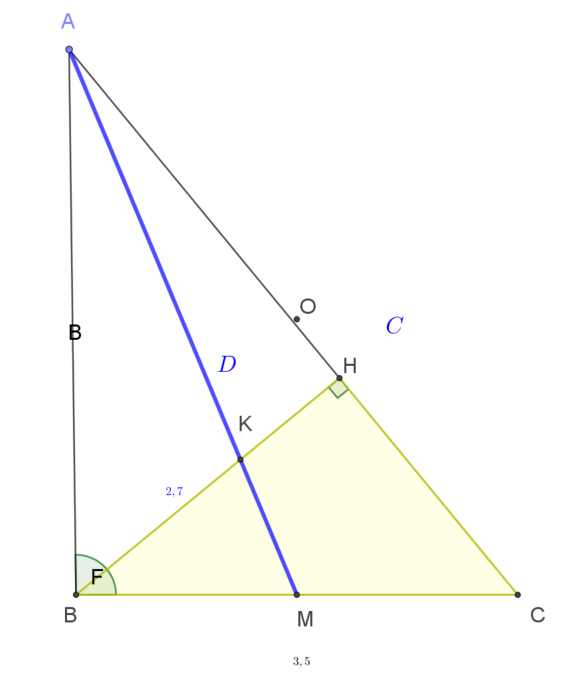
| 2019. Cho tam giác ABC có các góc A, C nhọn; BC = 3,5; đường cao BH = 2,7 và bán kính đường tròn ngoại tiếp bằng 2,8. Gọi K là giao điểm của BH và trung tuyến AM. Tính (chính xác đến 2 chữ số thập phân): a) Độ dài các cạnh AB, AC và trung tuyến AM của tam giác ABC. b) Bán kính R của đường tròn ngoại tiếp tam giác ABM. c) Diện tích S của tứ giác CHKM. |
|
Đáp án: $AB ≈ 4,32 ; AC \approx 5,60 ; AM ≈ 4,68 ; R≈ 2,34 ; S≈ 2,07$ |
a) Trong tam giác ABC: $\dfrac{BC}{\sin A}=2R\Rightarrow \widehat{A}=\sin^{-1}\dfrac{BC}{2R}$  lưu vào A.
lưu vào A.
Trong tam giác vuông ABH: $AB=\dfrac{BH}{\sin A}$  lưu vào B.
lưu vào B.
Trong tam giác ABC: $\widehat{ABC}=180^o-\widehat{BAC}-\widehat{ACB}$  lưu vào F.
lưu vào F.
$AC=2R\sin B=$ 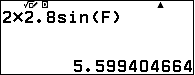 lưu vào C.
lưu vào C.
$AB^2+AC^2=2AM^2+\dfrac{BC^2}{2} \Rightarrow AM=$  lưu vào D.
lưu vào D.
b) Bán kính đường tròn ngoại tiếp tam giác ABM: $R=\dfrac{AM}{2\sin B}$  lưu vào E.
lưu vào E.
c) $S_{CMKH}=S_{BHC}-S_{BKM}=\dfrac12.BH.BC.\sin \widehat{HBC}-\dfrac12.BK.BM.\sin \widehat{HBC}$.
Áp dụng định lý Mê-nê-la-uyt vào tam giác BHC với cát tuyến AKM:
$$\dfrac{AH}{AC}.\dfrac{MC}{MB}.\dfrac{KB}{KH}=1⇔ \dfrac{AC-HC}{AC}.\dfrac{KB}{BH-BK}=1$$
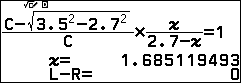
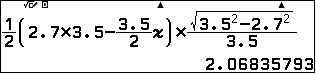
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay