BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Số nghiệm của phương trình hàm hợp, VDC Chuyên QH Huế
- 12/06/2021
- 78 lượt xem
Đặt $t=|x^2-1|-2$, đồ thị của $t$ theo $x$ như sau: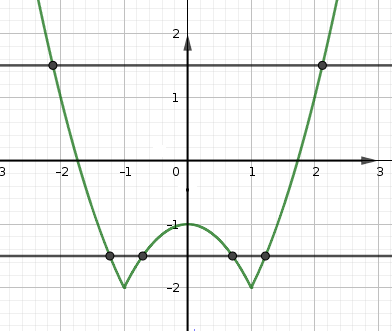 
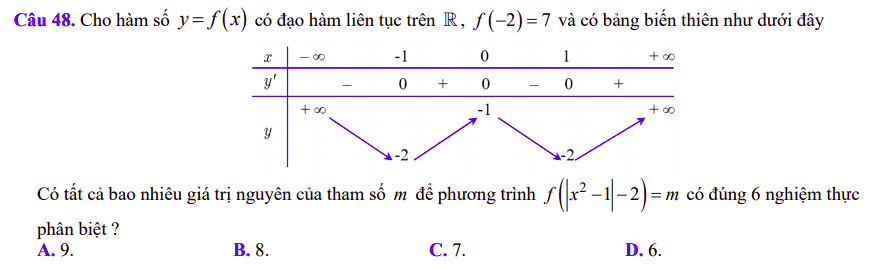
Ta thấy phương trình $f\left(\left|x^2-1\right|-2\right)=m$ có 6 nghiệm phân biệt khi và chỉ khi phương trình $f(t)=m$ có hai nghiệm trong đó có một nghiệm thuộc khoảng $(-2;-1)$ và một nghiệm lớn hơn $-1$.
Do $f(-2)=7$ nên nhìn vào bảng biến thiên ta thấy muốn phương trình $f(t)=m$ có nghiệm thuộc khoảng $(-2;-1)$ thì $m$ phải thuộc khoảng $(-2;7)$.
- 1. Nếu $m=-2$ phương trình $f(t)=-2 $ có hai nghiệm $t=\pm 1$ khi đó nhìn vào đồ thị của $t$ theo $x$ ta thấy phương trình đã cho có 5 nghiệm. (không thoả ycbt)
- 2. Nếu $m=-1$ phương trình $f(t)=-1 $ có ba nghiệm $t=0, t=t_1, t=t_2, -2<t_1<-1, t_2>1$ khi đó nhìn vào đồ thị của $t$ theo $x$ ta thấy phương trình đã cho có 8 nghiệm ($0, t_2$ mỗi giá trị sinh ra 2 nghiệm, $t_1$ sinh ra 4 nghiệm). (không thoả ycbt)
- 3. Nếu $m=7$ phương trình $f(t)=7 $ có hai nghiệm $t=-2, t=t_1 (t_1>1)$ khi đó nhìn vào đồ thị của $t$ theo $x$ ta thấy phương trình đã cho có 4 nghiệm ($-2, t_1$ mỗi giá trị sinh ra 2 nghiệm, . (không thoả ycbt)
- 4. Nếu $m=0,1,2,3,4,5,6,$ phương trình $f(t)=m$ có hai nghiệm $t_1, t_2$ trong đó $-2<t_1<-1, t_2>1$ nên phương trình đã cho có 6 nghiệm.
Vậy có 7 giá trị nguyên của $m$ để phương trình đã cho có 6 nghiệm thực phân biệt. Ta chọn C.
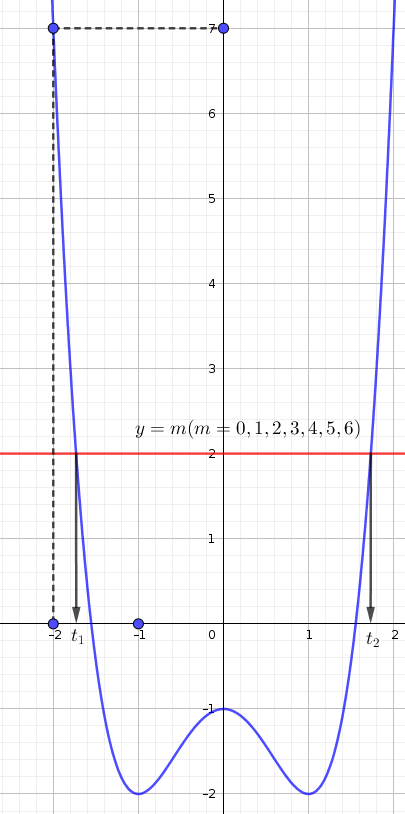
Nhận xét: Bài toán này chủ yếu nhìn vào đồ thị. Có thể tham khảo đồ thị (phác hoạ) như sau:
$t_1$ sinh ra 4 nghiệm $x$, $t_2$ sinh ra 2 nghiệm $x$.
Chia sẻ
About TS. Nguyễn Thái Sơn
