Thể tích của khối tứ diện khi biết 6 cạnh bởi định thức cấp 4
- 05/05/2023
- 446 lượt xem
|
Công thức
|
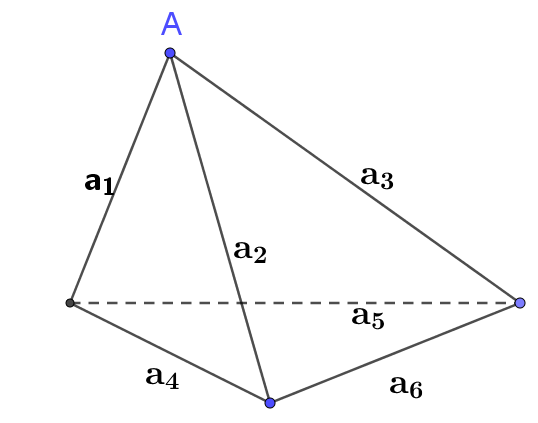
| Giả sử ta có một khối tứ diện, ba cạnh đi qua một đỉnh (giả sử đỉnh A) lần lượt ký hiệu là $a_1, a_2, a_3$.
Quy ước cạnh đối diện với $a_3, a_2, a_1$ lần lượt là $a_4, a_5, a_6$.
Lưu ý ba cạnh $a_1, a_4, a_5$; $\quad a_2, a_4, a_6$; $\quad a_3, a_5, a_6$ cùng đi qua một đỉnh (liệt kê tuân theo thứ tự, cố gắng nhớ thứ tự này) . Ta ký hiệu $A_i=a_i^2\quad (i=1,2,3,4,5,6)$. Ta xây dựng định thức cấp 4 sau đây, người ta gọi nó là định thức Caylay-Menger. Để dễ nhớ chúng tôi viết tuần tự: $$\left|\begin{array}{cccc}1 &1&1&1\\ Nhớ lại nhận xét về $a_1, a_4, a_5$. Cuối cùng nhớ lại nhận xét về $a_3, a_5, a_6$.$$D=\left|\begin{array}{cccc}1 &1&1&1\\ Định thức này là một số âm và thể tích của khối tứ diện: Định thức Caylay-Menger (gốc) là một số dương và là định thức cấp 5 (khá dễ nhớ, nhưng vì máy tính Casio fx-880BTG chỉ tính được định thức cấp 4 nên chúng tôi phải thay thế, khó nhớ hơn một chút). |
| Áp dụng |
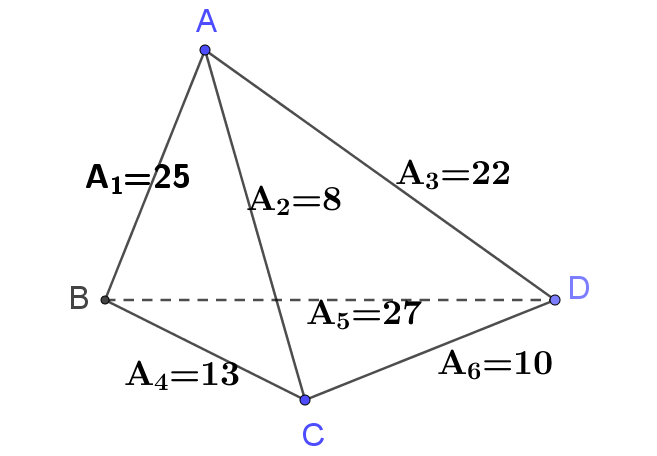
| Cho khối tứ diện ABCD có ${\color{blue} {AB=5}}, CD=\sqrt{10}, {\color{blue} {AC=2\sqrt2}}, BD=3\sqrt3, BC=\sqrt{13}, {\color{blue}{AD=\sqrt{22}}}$. Tính thể tích của khối tứ diện đã cho |
Mở một ma trận A cấp 4, nhìn vào hình không gian nhập tuần tự như hình vẽ dưới đây:

Cuối cùng lộ diện ma trận A:
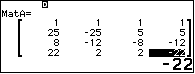
Và thể tích của khối tứ diện:

| Nhận xét: Máy tính Casio fx-9860 tính được định thức cấp 5, tuy nhiên nhập vào ma trận cấp 4 sẽ nhanh hơn nhập vào ma trận cấp 5. |
| Ngoài cách nhập trực tiếp ma trận A như trên (hơi khó nhớ) ta có nhập ma trận B và ma trận C như sau (riêng ma trận C chúng tôi nhập tuần tự cho dễ thực hiện): $$B=\left(\begin{array}{cccc} 1&1&1&1\\ A_1&-A_1&-A_2&-A_3\\ A_2&-A_1&-A_2&-A_3\\ A_3&-A_1&-A_2&-A_3 \end{array}\right)$$ $$\left(\begin{array}{cccc} Nhớ đặt bộ ba $A_4, A_5, A_6$ vào đúng chỗ. Lúc bấy giờ lấy $B+C$ ta được $A$. Cách này có thể thiết lập A nhanh hơn. |
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay