BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG GIẢI BÀI TOÁN TIẾP TUYẾN
- 12/04/2023
- 597 lượt xem
Đề bài: Cho hàm số $f(x)=x^3-6x^2+12x-8$ tiếp tuyến tại điểm có hoành độ thỏa phương trình $2y’-xy”=0$. Tiếp tuyến đi qua điểm nào sau đây:
A. $(2;-5)$ B. $(-2;0)$ C. $(0;3)$ D. $(-3;2)$
Lời giải
ta có $f(x)=x^3-6x^2+12x-8$
$\Rightarrow f'(x)=3x^2-12x+12$
$\Rightarrow f”(x)=6x-12$
Mở tính năng Solver
Tìm giá trị của phương trình $2y’-xy”=0$
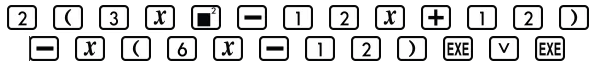
Lưu giá trị vào $A$
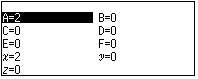
Mở tính năng Phép tính thường (Calculate)
Sử dụng tính năng Function
+ Lưu hàm số $f(x)=x^3-6x^2+12x-8$
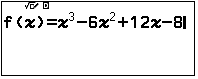
+ Lưu hàm số $g(x)=f'(A)(x-A)+f(A)$
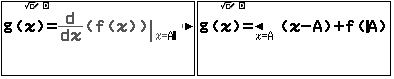
Mở tính năng bảng giá trị (Table)
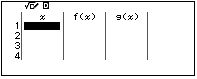
Chuyển về chế độ $g(x)$
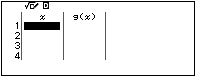
Tính giá trị của $g(x)$ khi $x$ chạy từ $-5$ đến $5$ với bước nhảy bằng $1$
Ta dễ dàng thấy phương trình tiếp tuyến chính là trục $Ox$
Vậy phương trình tiếp tuyến đi qua điểm có tọa độ $(-2;0)$
Chọn B
Lưu ý: Khoảng giá trị của $x$ và bước nhảy sẽ dựa vào đáp án để lựa chọn sao cho phù hợp
Chia sẻ
About Toanbitexdtgd1
