BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
THỰC HIỆN GIẢI MỘT SỐ CÂU TRONG ĐỀ THI THPT QG BẰNG MÁY TÍNH CASIO FX-580VN X
- 13/08/2020
- 278 lượt xem
Hướng dẫn giải lại một số câu trong đề thi THPT QG 2020 bằng máy tính Casio fx-580VN X.
Câu 2(MĐ101). Nghiệm của phương trình ${{3}^{x-1}}=9$ là:
| A. $x=-2$. | B. $x=3$. | C. $x=2$. | D. $x=-3$. |
Lời giải
Sử dụng Shift Solve:
Chọn B .
Câu 6(MĐ101). Số phức liên hợp của số phức $z=-3+5i$ là:
| A. $\bar{z}=-3-5i$. | B. $\bar{z}=3+5i$. | C. $\bar{z}=-3+5i$. | D. $\bar{z}=3-5i$. |
Lời giải
Chọn A .
Câu 13(MĐ101). Nghiệm của phương trình ${{\log }_{3}}\left( x-1 \right)=2$ là
| A. $x=8$. | B. $x=9$. | C. $x=7$. | D. $x=10$. |
Lời giải
Sử dụng Shift Solve:
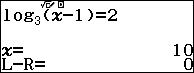
Chọn D.
Câu 22(MĐ101). Cho hai số phức ${{z}_{1}}=3-2i$ và ${{z}_{2}}=2+i$. Số phức ${{z}_{1}}+{{z}_{2}}$ bằng
| A. $5+i$. | B. $-5+i$. | C. $5-i$. | D. $-5-i$. |
Lời giải
Sử dụng tính năng số phức để thử nghiệm:
Ta có: ${{z}_{1}}+{{z}_{2}}=3-2i+2+i=5-i$.
Chọn C.
Câu 31(MĐ101). Gọi ${{z}_{0}}$ là nghiệm phức có phần ảo dương của phương trình ${{z}^{2}}+6z+13=0$. Trên mặt phẳng tọa độ, điểm biểu diễn số phức $1-{{z}_{0}}$ là
| A. $N\left( -2\,;\,2 \right)$. | B. $M\left( 4\,;\,2 \right)$. | C. $P\left( 4\,;\,-2 \right)$. | D. $Q\left( 2\,;\,-2 \right)$. |
Lời giải
Ta có: ${{z}^{2}}+6z+13=0\Leftrightarrow \left[ \begin{aligned} & z=-3+2i \\ & z=-3-2i \\\end{aligned} \right.$.
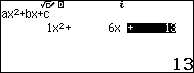
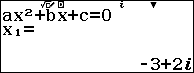
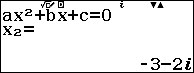
Do đó ${{z}_{0}}=-3+2i\Rightarrow 1-{{z}_{0}}=4-2i$.
Vậy ta chọn C.
Câu 34(MĐ101).Tập nghiệm của bất phương trình ${{3}^{{{x}^{2}}-13}}<27$ là
| A. $\left( 4\,;\,+\infty \right)$. | B. $\left( -4\,;\,4 \right)$. | C. $\left( -\infty \,;\,4 \right)$. | D. $\left( 0\,;\,4 \right)$. |
Lời giải
Sử dụng thử đáp án để giải bất phương trình :
Thử đáp án với $x=5$ :
Loại A.
Thử đáp án với $x=-3;x=3$ :
Loại D.
Thử đáp án với $x=-5$:
Loại C.
Vậy ta chọn B.
Câu 36(MĐ101). Giá trị nhỏ nhất của hàm số $f\left( x \right)={{x}^{3}}-24x$ trên đoạn $\left[ 2;19 \right]$ bằng
| A. $32\sqrt{2}$. | B. $-40$. | C. $-32\sqrt{2}$. | D. $-45$. |
Lời giải
Chọn C.
Nhập phương trình đã cho vào Phương thức phương trình/ hệ phương trình:
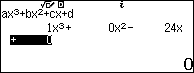
Tính giá trị 2 cận ta được:
Vậy giá trị nhỏ nhất trong đoạn $\left[ 2;19 \right]$ là $-32\sqrt{2}$.
Câu 47(MĐ101). Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$ và $O$ là tâm của đáy. Gọi $M$,$N$, $P$, $Q$ lần lượt là các điểm đối xứng với $O$ qua trọng tâm của các tam giác $SAB$, $SBC$, $SCD$, $SDA$ và $S’$ là điểm đối xứng với $S$ qua $O$. Thể tích của khối chóp $S’.MNPQ$ bằng
| A. $\dfrac{20\sqrt{14}{{a}^{3}}}{81}$. | B. $\dfrac{40\sqrt{14}{{a}^{3}}}{81}$. | C. $\dfrac{10\sqrt{14}{{a}^{3}}}{81}$. | D. $\dfrac{2\sqrt{14}{{a}^{3}}}{9}$. |
Lời giải
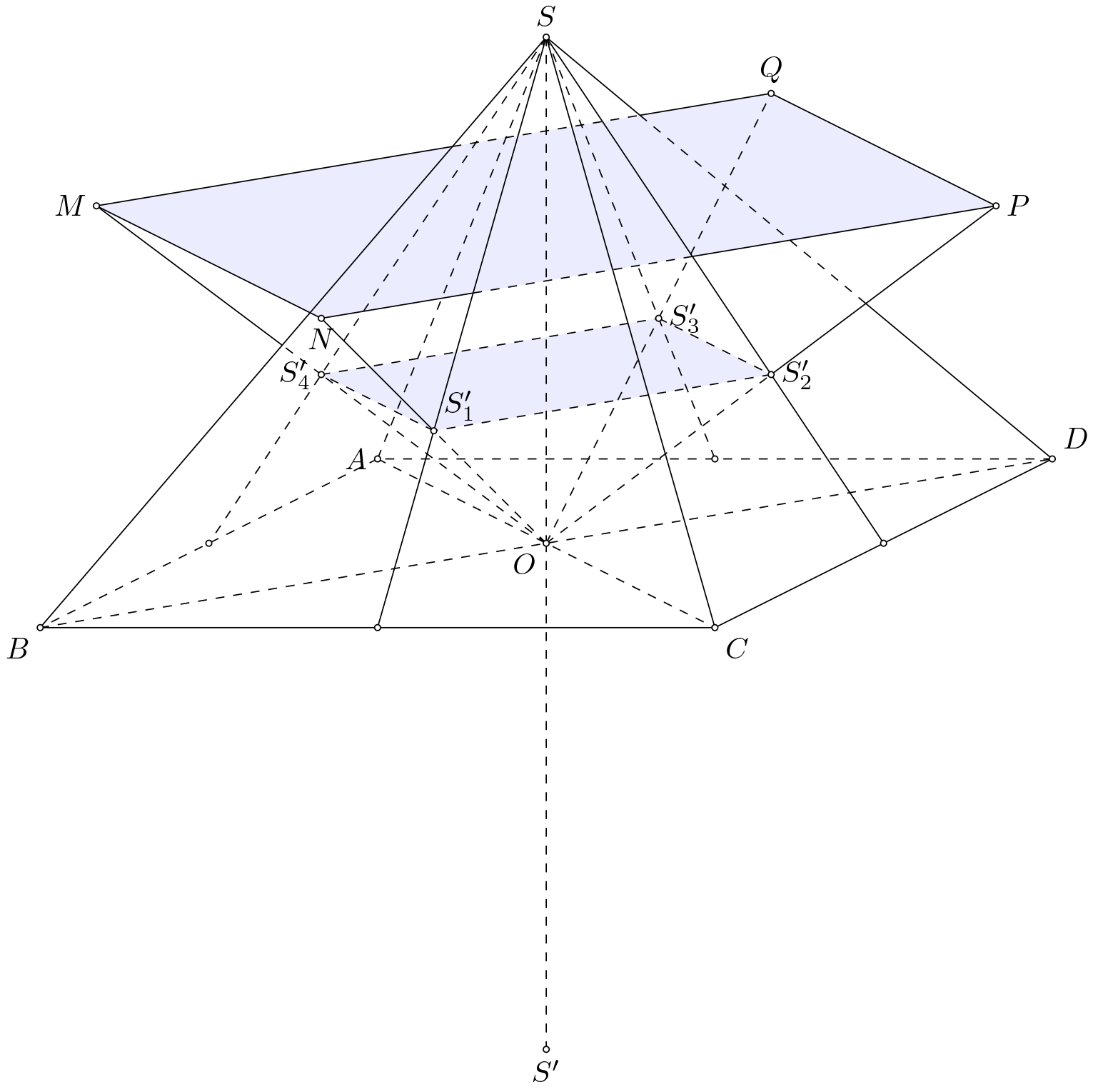
Chọn A.
Ghép hệ trục tọa độ ta được :
$O\left( 0;0;0 \right);S\left( 0;0;a\sqrt{3} \right);A\left( \dfrac{a\sqrt{2}}{2};0;0 \right);B\left( 0;\dfrac{a\sqrt{2}}{2};0 \right);C\left( -\dfrac{a\sqrt{2}}{2};0;0 \right);D\left( 0;-\dfrac{a\sqrt{2}}{2};0 \right)$
Gọi ${{S}_{1}};{{S}_{2}};{{S}_{3}};{{S}_{4}}$ lần lượt là trọng tâm của các tam giác $SAB$, $SBC$, $SCD$, $SDA$. Ta được:
$${{S}_{1}}\left( \dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{3}}{3} \right);{{S}_{2}}\left( -\dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{3}}{3} \right);$$
$${{S}_{3}}\left( -\dfrac{a\sqrt{2}}{6};-\dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{3}}{3} \right);{{S}_{4}}\left( \dfrac{a\sqrt{2}}{6};-\dfrac{a\sqrt{2}}{6};\dfrac{a\sqrt{3}}{3} \right)$$
Từ đó ta có được tọa độ của các đỉnh $S’,M,N,P,Q$ như sau :
$$S’\left( 0;0;-a\sqrt{3} \right);$$
$$M\left( \dfrac{a\sqrt{2}}{3};\dfrac{a\sqrt{2}}{3};\dfrac{2a\sqrt{3}}{3} \right);N\left( -\dfrac{a\sqrt{2}}{3};\dfrac{a\sqrt{2}}{3};\dfrac{2a\sqrt{3}}{3} \right);$$
$$P\left( -\dfrac{a\sqrt{2}}{3};-\dfrac{a\sqrt{2}}{3};\dfrac{2a\sqrt{3}}{3} \right);Q\left( \dfrac{a\sqrt{2}}{3};-\dfrac{a\sqrt{2}}{3};\dfrac{2a\sqrt{3}}{3} \right)$$
Như vậy, ta có được tọa độ các vector :
$$\begin{aligned} & \overrightarrow{S’M}=\left( \dfrac{a\sqrt{2}}{3};\dfrac{a\sqrt{2}}{3};\dfrac{5a\sqrt{3}}{3} \right);\overrightarrow{S’N}=\left( -\dfrac{a\sqrt{2}}{3};\dfrac{a\sqrt{2}}{3};\dfrac{5a\sqrt{3}}{3} \right); \\ & \overrightarrow{S’P}=\left( -\dfrac{a\sqrt{2}}{3};-\dfrac{a\sqrt{2}}{3};\dfrac{5a\sqrt{3}}{3} \right);\overrightarrow{S’Q}=\left( \dfrac{a\sqrt{2}}{3};-\dfrac{a\sqrt{2}}{3};\dfrac{5a\sqrt{3}}{3} \right) \\\end{aligned}$$
Sử dụng máy tính để nhập 4 vector vào:
Sử dụng máy tính để tính thể tích khối
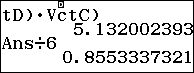
Vậy ta có thể tích khối chóp $S’.MNPQ$ là :
$$\begin{aligned} {{V}_{S’.MNPQ}}&={{V}_{S’.MNP}}+{{V}_{S’.MQP}} \\ & =\dfrac{1}{6}\left| \left[ \overrightarrow{S’M},\overrightarrow{S’N} \right].\overrightarrow{S’P} \right|+\dfrac{1}{6}\left| \left[ \overrightarrow{S’M},\overrightarrow{S’Q} \right].\overrightarrow{S’P} \right|=\dfrac{40\text{a}\sqrt{3}}{81} \end{aligned}$$
Chọn câu A.
About Bitex Khánh Vũ
