BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG CASIO fx 580VNX ĐỂ GIẢI NHANH PHƯƠNG TRÌNH LƯỢNG GIÁC BẬC NHẤT SIN, COS
- 27/08/2019
- 3,720 lượt xem
Phương trình bậc nhất đối với sin và cos là một dạng phương trình thường gặp trong chương trình Toán lớp 11. Do đó, trong bài viết này Diễn đàn Toán Casio sẽ hướng dẫn các bạn một “thủ thuật” dùng máy tính CASIO fx 580VNX để giải nhanh phương trình này.
Định nghĩa
Phương trình lượng giác bậc nhất theo $\sin ,\cos $ có dạng: $a\sin x+b\cos x=c$ với $a,b,c\in \mathbb{R}$ và ${{a}^{2}}+{{b}^{2}}\ne 0$
Phương pháp giải tổng quát:
Điều kiện có nghiệm của phương trình: ${{a}^{2}}+{{b}^{2}}\ge {{c}^{2}}$
Chia hai vế của phương trình cho $\sqrt{{{a}^{2}}+{{b}^{2}}}$ ta được:
$\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\sin x+\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\cos x=\dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Đặt $\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\cos \alpha $ , $\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\sin \alpha $ với $\alpha \in \left[ 0;2\pi \right)$
Khi đó, phương trình đã cho trở thành:
$\sin x.\cos \alpha +\cos x.\sin \alpha =\dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ $\Leftrightarrow \sin \left( x+\alpha \right)=\dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
đưa về phương trình lượng giác cơ bản
Phương pháp sử dụng máy tính Casio fx 580VNX
Thực hiện biến đổi phương trình bậc nhất theo $\sin ,\cos $ về dạng phương trình lượng giác cơ bản
$a\sin x+b\cos x=c\Leftrightarrow \sin \left( x+Y \right)=\dfrac{c}{X}$
Để thực hiện phép biến đổi trên ta sử dụng lệnh $Pol\left( a,b \right)$ với $a,b$ là các hệ số của phương trình. Khi đó, các giá trị $X,Y$sẽ tự động được lưu vào các ô nhớ $x,y$ của máy.
Bài toán. Giải các phương trình sau:
Câu 1. $\sqrt{3}\sin x+\cos x=1$
Câu 2. $\sqrt{3}\sin x-\cos x=\sqrt{2}$
Câu 3. $5\sin 2x+12\cos 2x=13$
Hướng dẫn giải
Câu 1. $\sqrt{3}\sin x+\cos x=1$
Bước 1. Chuyển máy tính về chế độ Radian qw22
Bước 2. Chuyển đổi phương trình đã cho về dạng phương trình lượng giác cơ bản
Tính $Pol\left( \sqrt{3},1 \right)$: q+s3$q)1=
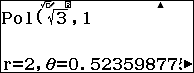qJ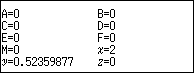
Kiểm tra lại giá trị Y: Q)= 
Như vậy ta có: $\sqrt{3}\sin x+\cos x=1\Leftrightarrow \sin \left( x+\dfrac{\pi }{6} \right)=\dfrac{1}{2}\left( * \right)$
Bước 3. Giải phương trình lượng giác cơ bản
Ấn qj1P2= 
Vậy:
$\left( * \right)\Leftrightarrow \sin \left( x+\dfrac{\pi }{6} \right)=\sin \left( \dfrac{\pi }{6} \right)$
$\Leftrightarrow \left[ \begin{align} & x+\dfrac{\pi }{6}=\dfrac{\pi }{6}+k2\pi \\ & x+\dfrac{\pi }{6}=\pi -\dfrac{\pi }{6}+k2\pi \\\end{align} \right.$
$\Leftrightarrow \left[ \begin{align} & x=k2\pi \\ & x=\dfrac{2\pi }{3}+k2\pi \\\end{align} \right.,\left( k\in \mathbb{Z} \right)$
Câu b. $\sqrt{3}\sin x-\cos x=\sqrt{2}$
Bước 1. Chuyển máy tính về chế độ Radian qw22
Bước 2. Chuyển đổi phương trình đã cho về dạng phương trình lượng giác cơ bản
Tính $Pol\left( \sqrt{3},-1 \right)$: q+s3$q)p1=
Kiểm tra lại giá trị Y: Q)=
Như vậy ta có: $\sqrt{3}\sin x-\cos x=\sqrt{2}\Leftrightarrow \sin \left( x-\dfrac{\pi }{6} \right)=\dfrac{\sqrt{2}}{2}\left( * \right)$
Bước 3. Giải phương trình lượng giác cơ bản
Ấn qjas2R2=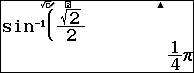
Vậy:
$\left( * \right)\Leftrightarrow \sin \left( x-\dfrac{\pi }{6} \right)=\sin \left( \dfrac{\pi }{4} \right)$
$\Leftrightarrow \left[ \begin{align} & x-\dfrac{\pi }{6}=\dfrac{\pi }{4}+k2\pi \\ & x-\dfrac{\pi }{6}=\pi -\dfrac{\pi }{4}+k2\pi \\\end{align} \right.$
$\Leftrightarrow \left[ \begin{align} & x=\dfrac{5\pi }{12}+k2\pi \\ & x=\dfrac{11\pi }{12}+k2\pi \\\end{align} \right.,\left( k\in \mathbb{Z} \right)$
Câu c. $5\sin 2x+12\cos 2x=13$
Bước 1. Chuyển máy tính về chế độ Radian qw22
Bước 2. Chuyển đổi phương trình đã cho về dạng phương trình lượng giác cơ bản
Tính $Pol\left( 5;12 \right)$: q+5q)12=
Ta có $X=\sqrt{{{a}^{2}}+{{b}^{2}}}=13$, như vậy $Y=\arccos \left( \dfrac{5}{13} \right)$
Như vậy ta có $5\sin 2x+12\cos 2x=13\Leftrightarrow \sin \left( 2x+\arccos \left( \dfrac{5}{13} \right) \right)=1\left( * \right)$
Bước 3. Giải phương trình lượng giác cơ bản
Ấn qj1= 
$\left( * \right)\Leftrightarrow \sin \left( 2x+\arccos \left( \dfrac{5}{13} \right) \right)=\sin \left( \dfrac{\pi }{2} \right)$
$\Leftrightarrow 2x+\arccos \left( \dfrac{5}{13} \right)=\dfrac{\pi }{2}+k2\pi$
$ \Leftrightarrow x=\dfrac{\pi }{4}-\dfrac{1 }{2}\arccos \left( \dfrac{5}{13} \right)+k\pi \left( k\in \mathbb{Z} \right)$
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
