BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG CASIO fx 580VNX ĐỂ GIẢI NHANH PHƯƠNG TRÌNH LƯỢNG GIÁC BẬC NHẤT SIN, COS- PHẦN 2
- 28/08/2019
- 682 lượt xem
Phương trình bậc nhất đối với sin và cos là một dạng phương trình thường gặp trong chương trình Toán lớp 11. Do đó, tiếp nối Phần 1, trong bài viết này Diễn đàn Toán Casio sẽ đưa ra thêm một vài bài toán luyện tập
Phương trình bậc nhất đối với sin và cos là một dạng phương trình thường gặp trong chương trình Toán lớp 11. Do đó, tiếp nối Phần 1, trong bài viết này Diễn đàn Toán Casiosẽ đưa ra thêm một vài bài toán luyện tập
Bài toán. Giải các phương trình sau:
Câu a. $\sin \left( \dfrac{\pi }{2}+2x \right)+\sqrt{3}\sin \left( \pi -2x \right)=2$
Câu b. $\cos x+\sqrt{3}\sin x+2\cos \left( 2x+\dfrac{\pi }{3} \right)=0$
Hướng dẫn giải
Câu a. $\sin \left( \dfrac{\pi }{2}+2x \right)+\sqrt{3}\sin \left( \pi -2x \right)=2$
Ta có: $\sin \left( \dfrac{\pi }{2}+2x \right)+\sqrt{3}\sin \left( \pi -2x \right)=2$$\Leftrightarrow \cos 2x+\sqrt{3}\sin 2x=2\left( * \right)$
Sử dụng máy tính Casio để đưa phương trình $\left( * \right)$ về dạng phương trình lượng giác cơ bản
Bước 1. Chuyển máy tính về chế độ Radian: qw22
Bước 2. Tính $Pol\left( \sqrt{3},1 \right)$: q+s3$q)1=
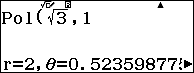
Kiểm tra giá trị của $Y$ Q)= 
Như vậy ta có:
$\cos 2x+\sqrt{3}\sin 2x=2$$\Leftrightarrow \sin \left( 2x+\dfrac{\pi }{6} \right)=1$
$\Leftrightarrow \sin \left( 2x+\dfrac{\pi }{6} \right)=\sin \left( \dfrac{\pi }{2} \right)$
$\Leftrightarrow 2x+\dfrac{\pi }{6}=\dfrac{\pi }{2}+k2\pi $
$\Leftrightarrow x=\dfrac{\pi }{6}+k\pi ,k\in \mathbb{Z}$
Câu b. $\cos x+\sqrt{3}\sin x+2\cos \left( 2x+\dfrac{\pi }{3} \right)=0$
Ta có $\cos x+\sqrt{3}\sin x+2\cos \left( 2x+\dfrac{\pi }{3} \right)=0$
$\Leftrightarrow \dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x=-\cos \left( 2x+\dfrac{\pi }{3} \right)$
$\Leftrightarrow \dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x=\cos \left( \pi -2x-\dfrac{\pi }{3} \right)$
$\Leftrightarrow \dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x=\cos \left( \dfrac{2\pi }{3}-2x \right)$
Sử dụng máy tính Casio để đưa phương trình về dạng phương trình lượng giác cơ bản
Bước 1. Chuyển máy tính về chế độ Radian qw22
Bước 2. Chuyển đổi phương trình đã cho về dạng phương trình lượng giác cơ bản
Tính $Pol\left( \dfrac{\sqrt{3}}{2};\dfrac{1}{2} \right)$ : q+as3R2$q)a1R2=
Kiểm tra giá trị $Y$: Q)=
Như vậy ta có:
$\dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x=\cos \left( \dfrac{2\pi }{3}-2x \right)$
$\Leftrightarrow \sin \left( x+\dfrac{\pi }{6} \right)=\cos \left( \dfrac{\pi }{2}+\dfrac{\pi }{6}-2x \right)$
$\Leftrightarrow \sin \left( x+\dfrac{\pi }{6} \right)=\sin \left( 2x-\dfrac{\pi }{6} \right)$
$\Leftrightarrow \left[ \begin{align} & x+\dfrac{\pi }{6}=2x-\dfrac{\pi }{6}+k2\pi \\ & x+\dfrac{\pi }{6}=\pi -\left( 2x-\dfrac{\pi }{6} \right)+k2\pi \\\end{align} \right.,k\in \mathbb{Z}$
$\Leftrightarrow \left[ \begin{align} & x=\dfrac{\pi }{3}-k2\pi \\ & x=\dfrac{\pi }{3}+\dfrac{k2\pi }{3} \\\end{align} \right.,k\in \mathbb{Z}$
$\Leftrightarrow x=\dfrac{\pi }{3}+\dfrac{k2\pi }{3},k\in \mathbb{Z}$
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
