BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI BÀI TOÁN THỰC TẾ LIÊN QUAN ĐẾN LOGARIT LỚP 11
- 26/01/2024
- 224 lượt xem
Đề bài: (Vân dụng trang 11 sách chân trời sáng tạo toán 11)
Độ lớn $M$ của một trận động đất theo thang Richter được tính theo công thức $M=\log \frac{A}{A_{0}}$. Trong đó $A$ là biên độ lớn nhất ghi được bởi máy đo địa chấn, $A_{0}$ là biên độ tiêu chuẩn được sử dụng để hiệu chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn với $A_{0}=1\mu $.
a) Tính độ lớn của trận động đất có biên độ A bằng
i) $10^{5,1}A_{0}$; ii) $65 000A_{0}$
b) Một trận động đất tại điểm $N$ có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại điểm $P$. So sánh độ lớn của hai trận động đất.
Lời giải
a)
Trên máy tính fx-880BTG để sử dụng tính năng $\log $ (log cở số 10) ta thực hiện thao tác như sau:
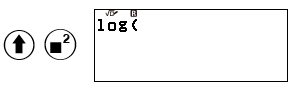
i) $M=\log \frac{A}{A_{0}}=\log \frac{10^{5,1}{A_{0}}}{A_{0}}=\log 10^{5,1}=5,1$
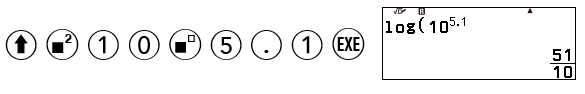
Để chuyển qua số thập phân ta thực hiện thao tác:
ii) $M=\log \frac{A}{A_{0}}=\log \frac{65000A_0}{A_{0}}=\log 65000\approx4,8$
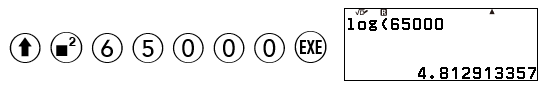
b)
Gọi $A_1$ là biên độ lớn nhất của trận động đất tại điểm $P$
$\Rightarrow $ biên độ lớn nhất của trận động đất tại điểm $N$ là $3A_1$
Độ lớn của trận động đất tại điểm $P$:
$M_P=\log \dfrac{A}{A_{0}}=\log \dfrac{A_1}{A_{0}}$
Độ lớn của trận động đất tại điểm $N$:
$M_N=\log \dfrac{A}{A_{0}}=\log \dfrac{3A_1}{A_{0}}=\log 3+ \log\dfrac{A_1}{A_{0}}=\log 3+M_P$
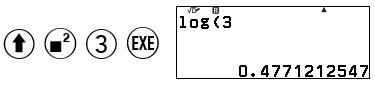
$\Rightarrow M_N \approx 0,48+M_P$
Vậy độ lớn của trận động đất tại $N$ lớn hơn độ lớn của trận động đất tại $P$
Chia sẻ
About Toanbitexdtgd1
