BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Về vấn đề giải phương trình vô tỉ trên MTCT
- 25/10/2021
- 152 lượt xem
| Tìm nghiệm gần đúng (chính xác đến 2 chữ số thập phân) của phương trình:$$\sqrt{2,7x-3,4}=4,5-1,9x$$ |
- 1. Theo ycbt ta hiểu phương trình này có một nghiệm duy nhất và ta đi tìm nghiệm gần đúng (chính xác đến 2 chữ số thập phân) của nó. Nếu vậy ta chỉ cần viết phương trình lên màn hình, bấm SHIFT SOLVE, vậy là xong như sau đây:
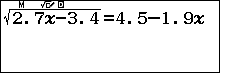
- 2. Tuy nhiên về phương diện giải bài toán này bằng phương pháp tự luận, ta tiến hành như sau:
$$\sqrt{2,7x-3,4}=4,5-1,9x\Leftrightarrow \left\{\begin{array}{l}4,5-1,9x\geqslant 0\\
2,7x-3.4=(4,5-1,9x)^2\end{array}\right.$$
Bấm MENU 912 với các hệ số $$\fbox{$1.9^2$} \quad \fbox{$-2\times 4.5\times 1.9-2.7$}\quad \fbox{$4.5^2+3.4$}$$
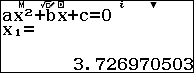
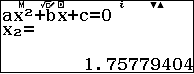
(trong đó nghiệm $x_1$ bị loại do vi phạm điều kiện) nên phương trình có nghiệm duy nhất $x_2=1,76$ (nếu làm tròn tới hai số lẻ thập phân) sau dấu phẩy.
Chia sẻ
About TS. Nguyễn Thái Sơn
