BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG KIỂM TRA SỐ NGUYÊN TỐ
- 07/09/2023
- 438 lượt xem
Một số nguyên là số nguyên tố khi và chỉ khi nó không chia hết cho số nguyên tố nào nhỏ hơn hay bằng căn bậc hai của nó.
Bài toán 1: Kiểm tra số $33915$ có là số nguyên tố hay không?
-
Nhập số $33915$
-
Phân tích thừa số nguyên tố của số $33915$
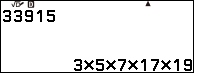
Đó là những trường hợp thừa số là những số có $3$ chữ số, vậy khi thừa số từ $4$ chữ số trở lên, ta sử dụng định lý sau:
* Định lý
Nếu $N$ là hợp số thì nó có thừa số nguyên tố $p$ thỏa mãn điều kiện: $p\leq N$
Bài toán 2: Kiểm tra số $1847$ có là số nguyên tố hay không?
Bước 1: Khai căn số $1847$
Ta được: $\sqrt{1847}\approx 42,98$. Theo định lý, nếu $1847$ không phải là số nguyên tố thì nó sẽ có ước nguyên tố $p\leq 42$
Bước 2: Kiểm tra bằng tính năng BẢNG TÍNH (SPREADSHEET)
-
-
Mở tính năng bảng tính
-
-
-
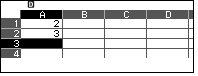
Nhập $2$, $3$ vào ô $A1$, $A2$
-
-
-
Sử dụng tính năng điền công thức (Fill Formula)
-
Dạng (Form) $=A2+2$
Phạm vi (Range): $A3:A22$
-
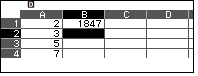
Nhập số $1847$ vào ô $B1$
-
Tại ô $C1$ Sử dụng tính năng điền công thức (Fill Formula)
Dạng (Form) $=B\$1:A1$
Phạm vi (Range): $C1:C22$
Bước 3: Duyệt bảng số liệu
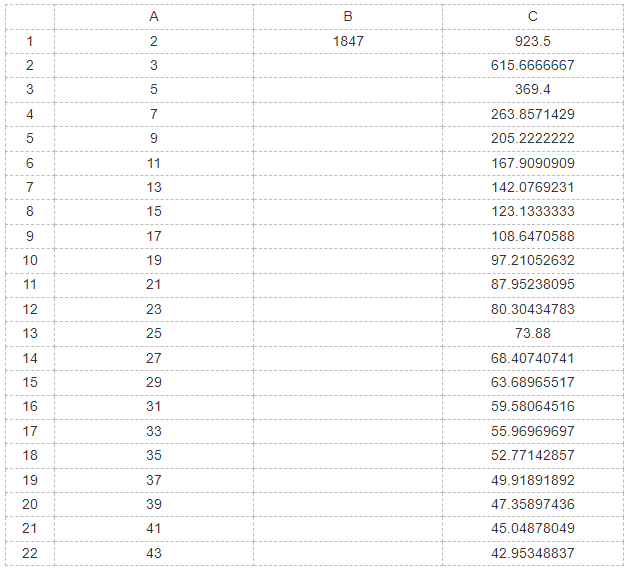
Nhận xét: $1847$ không chia hết cho $2$ và cũng không chia hết cho số lẻ nào nhỏ hơn hoặc bằng căn bậc $2$ của $1847$
Vậy $1847$ là số nguyên tố
Chia sẻ
About Toanbitexdtgd1
