BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG GIẢI BÀI TOÁN TÍNH GIÁ TRỊ BIỂU THỨC
- 07/09/2023
- 454 lượt xem
Bài 1: Tính giá trị biểu thức: $A=1+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{7+\dfrac{1}{9+\dfrac{1}{11+\dfrac{1}{13}}}}}}$
Lời giải
Bước 1: Mở tính năng BẢNG TÍNH (SPREADSHEET)
Bước 2: Điền lần lượt các giá trị $13,11,9,…,1$ vào các ô $A1,A2,A3,…A8$
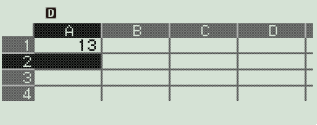
Nhập $13$ vào ô $A1$
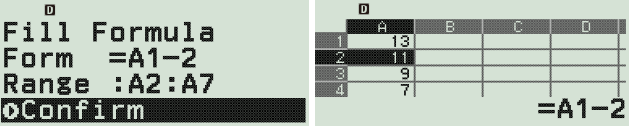
Sử dụng tính năng điền công thức (Fill Formula)
Dạng (Form) $=A2-2$
Phạm vi (Range): $A1:A7$
Bước 3: Ô $B2$ tính $\dfrac{1}{A1}+A2$
Bước 4: Sử dụng tính năng điền công thức (Fill Formula)
Dạng (Form) $=$
Phạm vi (Range): $B3:B8$
Bước 5: Duyệt bảng số liệu
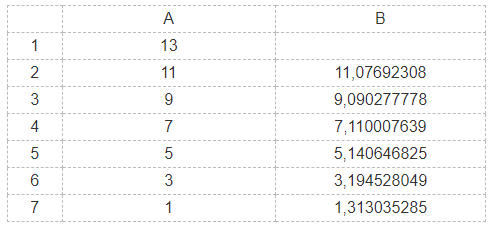
Vậy giá trị của biểu thức $A= 1,313035285$
Bài 2: Tính giá trị biểu thức $B=\sqrt[5]{2+\sqrt[5]{4+\sqrt[5]{6+\sqrt[5]{8+\sqrt[5]{10+\sqrt[5]{12+\sqrt[5]{14}}}}}}}$
Lời giải
Bước 1: Mở tính năng BẢNG TÍNH (SPREADSHEET)
Bước 2: Điền lần lượt các giá trị $14,12,10,…,2$ vào các ô $A1,A2,A3,…A7$
Nhập $14$ vào ô $A1$
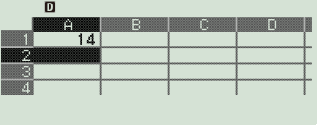
Sử dụng tính năng điền công thức (Fill Formula)
Dạng (Form) $=A1-2$
Phạm vi (Range): $A1:A7$
Bước 3: Ô $B2$ tính $\sqrt[5]{A1}+A2$
Bước 4: Sử dụng tính năng điền công thức (Fill Formula)
Dạng (Form) $=$
Phạm vi (Range): $B3:B7$
Bước 5: Duyệt bảng số liệu
Vậy giá trị của biểu thức $B= 3,406240732$
Bài 3: Cho hàm số $f(x)=\dfrac{x^2+2x+3}{\sqrt{2x+1}}$. Tính giá trị của biểu thức $C=f^2(2)+f(f(3))$
Lời giải
Bước 1: Sử dụng tính năng FUNCTION lưu biểu thức vào $f(x)$
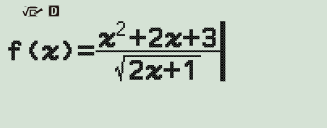
Bước 2: tính giá trị của biểu thức $C=f^2(2)+f(f(3))$
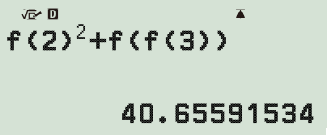
Vậy giá trị của biểu thức $C= 40,65591534$
Chia sẻ
About Toanbitexdtgd1
