BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG GIẢI BÀI TOÁN HỆ THỨC LƯỢNG TRONG TAM GIÁC (CTST)
- 12/09/2023
- 356 lượt xem
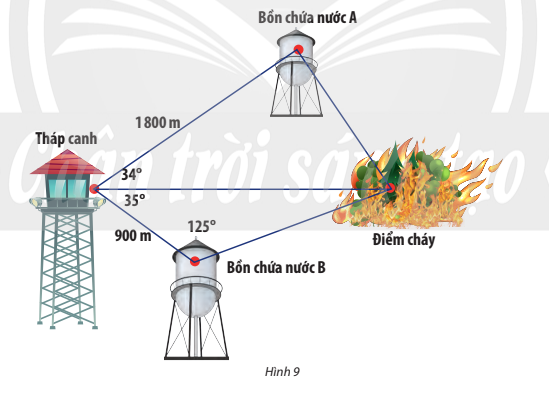
Bài 1: (Vận dụng 2 trang 69 sách chân trời sáng tạo) Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước $A, B$ để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như hình $9$. Nên dẫn nước từ buồn chứa $A$ hay $B$ để dập đám cháy nhanh hơn?
*Cách cài đặt máy tính fx-880BTG để tính giá trị lượng giác của một góc
Lời giải
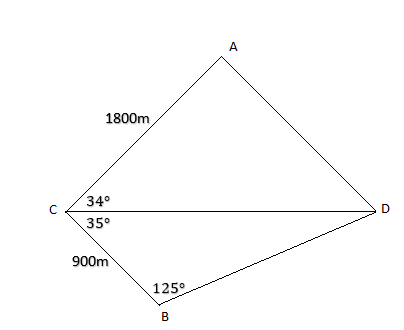
Xét $\Delta CBD$ ta có:
$\widehat{C}+\widehat{B}+\widehat{D}=180^{\circ}\\
\Rightarrow \widehat{D}=180^{\circ}-35^{\circ}-125^{\circ}=20^{\circ}$
Ta có $\dfrac{BC}{\sin \widehat{D}}=\dfrac{BD}{\sin \widehat{C}}\\$
$\Leftrightarrow \dfrac{900}{\sin 20^{\circ}}=\dfrac{BD}{\sin 35^{\circ}}\\
\\\Rightarrow BD=\dfrac{900.\sin 35^{\circ}}{\sin 20^{\circ}}\\$
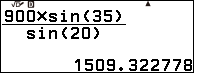
$\\ BD\approx 1509,32 m$
Khoảng cách từ buồn chứa nước $B$ đến đám cháy là $1509,32 m$
Ta có $\dfrac{BC}{\sin \widehat{D}}=\dfrac{CD}{\sin \widehat{B}}\\$
$\Leftrightarrow \dfrac{900}{\sin 20^{\circ}}=\dfrac{CD}{\sin 125^{\circ}}\\
\\\Rightarrow CD=\dfrac{900.\sin 125^{\circ}}{\sin 20^{\circ}}\\$
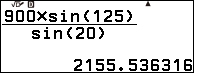
$\\CD\approx 2155,54 m$
Xét $\Delta ACD$ ta có:
$AD^2=AC^2+CD^2+2.AC.CD.\cos \widehat{C}\\
\Leftrightarrow AD^2=1800^2+2155,54^2-2.1800.2155,54.\cos 34^{\circ}\\$
$ AD^2\approx1453067,56\\$
$ AD=1205,43m$
Khoảng cách từ buồn chứa nước $A$ đến đám cháy là $1205,43 m$
Vậy nên dẫn nước từ bồn chứa $A$ để dập tắt đám cháy nhanh hơn
About Toanbitexdtgd1
