BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG GIẢI BÀI TOÁN HỆ THỨC LƯỢNG TRONG TAM GIÁC (KNTT)
- 13/09/2023
- 532 lượt xem
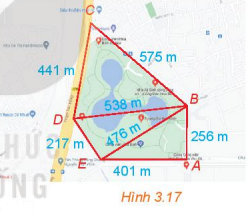
Đề bài: (Vận dụng 3 trang 43 sách kết nối tri thức lớp 10) Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác $ABCDE$ như hình $3.17$. Dùng chế độ tính khoảng cách giữa hai điểm của Google Maps, một người xác định được khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên Hòa Bình.
Lời giải
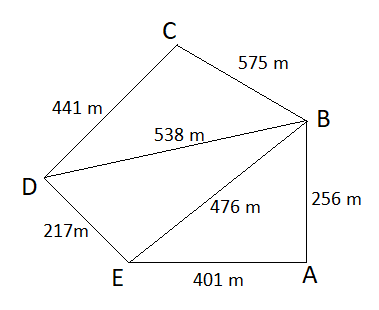
Để tính diện tích của ngũ giác $ABCDE$ ta tách ngũ giác thành $3$ tam giác $ABE$, $BDE$, $BCD$ sau đó tính diện tích của từng tam giác
Để tính diện tích của tam giác ta sử dụng công thức Heron:
$S=\sqrt{p(p-a)(p-b)(p-c)}$
Trong đó:
$a, b, c$: là ba cạnh của tam giác
$p=\dfrac{a+b+c}{2}$ là nửa chu vi của tam giác
Diện tích tam giác $ABE$
$p_{\Delta ABE}=\dfrac{AB+AE+BE}{2}=\dfrac{256+401+476}{2}=\dfrac{1133}{2}$
$S_{\Delta ABE}=\sqrt{p_{\Delta ABE}(p_{\Delta ABE}-AB)(p_{\Delta ABE}-AE)(p_{\Delta ABE}-BE)}\\$
$=\sqrt{\dfrac{1133}{2}(\dfrac{1133}{2}-256)(\dfrac{1133}{2}-401)(\dfrac{1133}{2}-476)}\\$
$\approx 51328$ $m$
Diện tích tam giác $BDE$
$p_{\Delta BDE}=\dfrac{BD+BE+DE}{2}=\dfrac{538+476+217}{2}=\dfrac{1231}{2}$
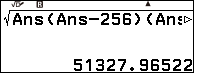
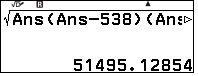
$S_{\Delta BDE}=\sqrt{p_{\Delta BDE}(p_{\Delta BDE}-BD)(p_{\Delta BDE}-BE)(p_{\Delta BDE}-DE)}\\$
$=\sqrt{\dfrac{1231}{2}(\dfrac{1231}{2}-538)(\dfrac{1231}{2}-476)(\dfrac{1231}{2}-217)}\\$
$\approx 51495$ $m$
Diện tích tam giác $BCD$
$p_{\Delta BCD}=\dfrac{BC+BD+CD}{2}=\dfrac{575+538+441}{2}=777$
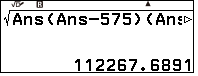
$S_{\Delta BCD}=\sqrt{p_{\Delta BCD}(p_{\Delta BCD}-BC)(p_{\Delta BCD}-BD)(p_{\Delta BCD}-CD)}\\$
$=\sqrt{777(777-575)(777-538)(777-441)}\\$
$\approx 112268$ $m$
Diện tích ngũ giác $ABCDE$
$S_{ABCDE}=S_{\Delta ABE}+S_{\Delta BDE}+S_{\Delta BCD}=215091$ $m$
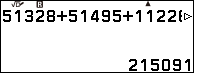
Vậy diện tích của công viên Hòa Bình là $215091$ $m^2$
Chia sẻ
About Toanbitexdtgd1
