BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG CHUYỂN SỐ THẬP PHÂN VÔ HẠN KHÔNG TUẦN HOÀN THÀNH CĂN THỨC
- 04/10/2023
- 1,111 lượt xem
| Đặt vấn đề: |
| Giả sử trong quá trình giải toán (thường là giải phương trình vô tỉ) mà ta gặp nghiệm $x$ là một số thập phân vô hạn không tuần hoàn, ta muốn chuyển nó thành một số thực dạng $A+B\sqrt{C}$ với $A, B$ là các số hữu tỉ và $C$ là số nguyên dương. |
Lưu ý: Ta không tuỳ ý thử một số $x$ nào đó, ta chỉ thử với $x$ là nghiệm của một phương trình, ví dụ giải phương trình sau bằng Solver trên MÁY TÍNH Casio fx-880BTG:$$\sqrt{x+20}=x-4$$
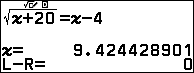
Trường hợp 1 (đơn giản): Sở dĩ chúng tôi gọi là đơn giản vì nghiệm $x$ nói trên là nghiệm của một phương trình bậc hai hệ số nguyên và hệ số của $x^2$ bằng $1$. Ta lưu số $x$ đó vào $x$ (nếu dùng Solver, máy tính tự động lưu vào $x$.)
Ta mở một Bảng tính, viết số $1$ vào $A1$, viết số $-22$ vào $B1$.
Dùng Fill Formular (Điền công thức) vào $B2:B45$ với công thức là $B1+1$. 
Đưa con trỏ tới $C1$, dùng Fill Formular (Điền công thức) vào $C1:C45$ với công thức là $A\$1x^2+B1x$ (ý muốn tính $Ax^2+Bx$)(chú ý có dấu $\$$ trước số $1$ để cố định A1). 
(chú ý dùng Tools để Hiện ô là Giá trị.)
Duyệt bảng tính đến dòng 14 thấy khi $B=-9$ thì $1x^2-9x=4$, nghĩa là $x$ là nghiệm dương của phương trình $x^2-9x-4=0 ⇔$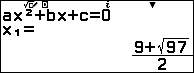
Trường hợp 2 (khó hơn): Khi không có phương trình bậc hai nào hệ số nguyên và hệ số của $x^2$ bằng 1.
Giả sử ta có số $x$ như sau mà máy tính đã tự động lưu vào $x$:
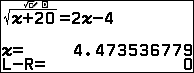
Lưu ý nếu bấm vào VARIABLES sẽ thấy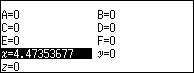 
Vào lại bảng tính, muốn sử dụng lại Thuật toán (nếu không thì phải Điền lại công thức cho cột C) ta bấm TOOLS, chọn 
rồi bấm AC để trở lại bảng tính.
Khi Bảng tính tự động tính lại, nó thấy $x$ đã thay đổi nên không thấy dòng nào có kết quả là số nguyên.
Ta đưa con trỏ tới $A1$ nhập số $2$, duyệt lại bảng tính không thấy dòng nào có kết quả là số nguyên.
Ta đưa con trỏ tới $A1$ nhập số $3$, duyệt lại bảng tính không thấy dòng nào có kết quả là số nguyên.
Ta đưa con trỏ tới $A1$ nhập số $4$, duyệt lại bảng tính thấy dòng 6 có kết quả là số nguyên: 
Điều đó có nghĩa là số $x$ là nghiệm dương của phương trình $4x^2-17x=4 ⇔ $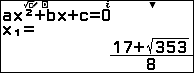 
| Giải thích thêm |
| 1. Mục đích của việc làm là đi tìm một phương trình bậc hai có dạng $ax^2+bx=c$ nhận số thập phân đang xét làm nghiệm (trường hợp đơn giản với $a=1$ và $b, c$ là các số nguyên cần tìm ). Khi đó chỉ cần bấm máy tính giải phương trình bậc hai này ta có số vô tỉ dạng căn thức. Đây là lý do thầy chọn 1 (hệ số của $x^2$) vào $A1$.
2. Để tìm số nguyên $b$ thầy cho $b$ chạy từ $-22$ đến $22$ vì Bảng giá trị hay Bảng tính đều dùng được tối đa 45 số hạng (45 số gần nhất có dương có âm). Đây là lý do thầy điền công thức từ B1 đến B45 cho $b$ chạy từ $-22$ đến $22$ như trong bài. Nếy may mắn (thường là may vì bài toán không thể quá phức tạp), thì $b$ nằm trong khoảng này.
3. Còn tại sao cột C thầy điền công thức như đã viết?. Trả lời: Vì $c=Ax^2+Bx$ với $A=1$. |
About TS. Nguyễn Thái Sơn
