Tính nhanh nhờ sử dụng các biến nhớ
- 24/10/2021
- 123 lượt xem
Trong kỳ thi học sinh giỏi MTCT cấp THCS của TP Hồ Chí Minh, việc giải nhanh một bài toán phổ biến sẽ tranh được thứ hạng cao thấp. Nếu sử dung các cách thức thông thường vẫn giải ra đáp số nhưng nếu giải nhanh hơn có thể sẽ có đủ thời gian để làm đến các câu cuối của bài thi. Sau đây là một ví dụ:
| Bài 9. Cho đa thức bậc ba $P (x )$ có $P(k )=\dfrac{k}{3k-1}, k= 1, 2, 3, 4$. Tính $P(24)$. |
Giải
Ta lần lượt lưu $1,2,3,4$ vào các biến nhớ A, B, C, D. Sau đó tính các hệ số $a, b,c, d$ của đa thức bậc ba $P(x)=ax^3+bx^2+cx+d$.
Sau đó mở trên máy tính một hệ 4 phương trình và nhập các biến $x$ lần lượt bằng A, B, C, D vào hệ phương trình:

Giải ra nghiệm
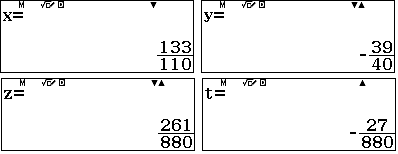
lần lượt đem lưu vào A, B, C, D. (ghi đè lên các biến nhớ). Sau đó viết đa thức bậc ba lên màn hình và bấm CALC rồi nhập $x=24$ và chấp nhận các giá trị A,B,C,D ta được $P(24)$ bằng:
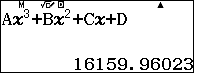
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay