Một phương pháp thực dụng giải phương trình vô tỉ
- 18/10/2022
- 331 lượt xem
trong bài thi 10 chuyên TP HCM và HN từ 2015 -2022
|
1. Năm 2022 $\qquad \sqrt{x+4}+|x|=x^2-(x+4)$
2. Năm 2020 $\qquad \sqrt{2x^2+x+9}+\sqrt{2x^2-x+1}=x+4$
3. Năm 2019 $\qquad 5\sqrt{x-1}-\sqrt{x+7}=3x-4$
4. Năm 2018 $\qquad 4\sqrt{x+3}=1+4x+\dfrac{2}{x}$
5. Năm 2017 $\qquad 2(x+2)\sqrt{3x-1}=3x^2-7x-3$
6. Năm 2016 $\qquad x^2-6x+4+2\sqrt{2x-1}=0$
7. Năm 2015 $\qquad 2x^2+x+3=3x\sqrt{x+3}$
|
Sở dĩ chúng tôi dùng từ “thực dụng” vì nó sẽ bỏ qua mọi suy luận nhằm biến đổi phương trình đã cho về dạng đơn giản hơn mà chỉ cần bình phương hai vế dẫn tới phương trình bậc 4 và sử dụng máy tính. Việc nhanh chóng hoàn thành lời giải sẽ tiết kiệm thời gian cho các câu còn lại.
|
1. Công việc chuẩn bị máy tính Casio fx-880BTG: Cài đặt Digit Separator ON
2. Phương pháp:
Đặt VT $=f(x)$ và VP $=g(x)$ thích hợp lưu vào các biến nhớ f(x), g(x)
Sau đó bình phương hai vế dẫn đến phương trình bậc bốn. Tiếp theo dùng hệ thức Vi-et đưa đến tích của hai phương trình bậc hai.
Tìm các nghiệm và thử lại nghiệm.
|
Năm 2015: Giải phương trình $\qquad 2x^2+x+3=3x\sqrt{x+3}\quad (1)$
Điều kiện: $x>0$, bình phương hai vế phương trình (1):
$$(2x^2+x+3)^2=\left(3x\sqrt{x+3}\ \right)^2 \Leftrightarrow 4x^4-5x^3-14x^2+6x+9=0\quad (2)$$

Bấm MTCT xuất ra 4 nghiệm lần lượt lưu vào A, B, C, D.


$$(2)\Leftrightarrow 4(x^2-x-3)\left(x^2-\dfrac14x-\dfrac34\right)=0 \Leftrightarrow \left[\begin{array}{lll}
x&=&\dfrac{1+\sqrt{13}}{2}\\
x&=&\dfrac{1-\sqrt{13}}{2}\quad \text{(loại)}\\
x&=&1\\
x&=&-\dfrac34 \quad \text{(loại)}
\end{array}
\right.$$
|
Lời giải: Điều kiện: $x>0$, bình phương hai vế phương trình (1):
|
Năm 2016: Giải phương trình $\qquad x^2-6x+4+2\sqrt{2x-1}=0\quad (1)$
$$(1)\Leftrightarrow 2\sqrt{2x-1}=-x^2+6x-4\quad (2)$$
Điều kiện: $-x^2+6x-4\geqslant 0 \Leftrightarrow $ 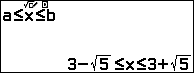
Bình phương hai vế:
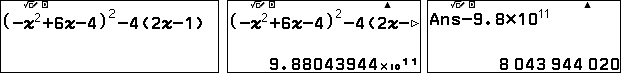
$$(2) \Leftrightarrow x^4-12x^3+44x^2-56x+20=0\quad (3)$$


$$(3)\Leftrightarrow (x^2-8x+10)(x^2-4x+2)=0 \Leftrightarrow \left[\begin{array}{lll}
x&=& 4+ \sqrt6\quad \text{(loại)}\\
x&=&4- \sqrt6\\
x&=&2+\sqrt2\\
x&=&2-\sqrt2\quad \text{(loại)}\\
\end{array}
\right.$$
|
Lời giải: $$(1)\Leftrightarrow 2\sqrt{2x-1}=-x^2+6x-4\quad (2)$$
Điều kiện: $-x^2+6x-4\geqslant 0 \Leftrightarrow 3-\sqrt5\leqslant x\leqslant 3+\sqrt5$. Bình phương hai vế phương trình (2):
|
Năm 2017 $\qquad 2(x+2)\sqrt{3x-1}=3x^2-7x-3$
Điều kiện: Bài này ta không đặt điều kiện và sẽ thử lại nghiệm sau khi tìm được các nghiệm đó.
Bình phương hai vế phương trình đã cho ta có:


$$9x^4-54x^3-13x^2+10x+25=0$$


$$\Leftrightarrow (x^2-7x+5)(9x^2+9x+5=0)=0\Leftrightarrow \left[\begin{array}{lll}
x^2-7x+5&=&0\\
9x^2+9x+5&=&0 \quad \text{(vô nghiệm)}
\end{array}
\right.$$
|
Lời giải: $$(1)\Leftrightarrow 2(x+2)\sqrt{3x-1}=3x^2-7x-3$$
Bình phương hai vế phương trình ta có: Thay hai giá trị vừa tìm được vào phương trình đã cho ta có:
Vậy phương trình có một nghiệm duy nhất $$x=\dfrac{7+\sqrt{29}}{2}$$
|
Năm 2019 $\qquad 5\sqrt{x-1}-\sqrt{x+7}=3x-4 \quad (1)$
Bình phương hai vế và thu gọn phương trình (1): $$-9x^2+50x-37=10\sqrt{x^2+6x-7}$$
Tiếp tục bình phương hai vế và thu gọn phương trình (2):
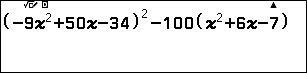

$$81x^4-900x^3+3012x^2-4000x+1856=0$$

Vì tích của 4 nghiệm bằng $\dfrac{e}{a}$ nên nghiệm kép là 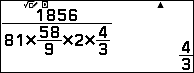
Vậy phương trình được viết: $$81\left(x-\dfrac43\right)^2\left(x^2-\dfrac{76}{9}x+\dfrac{116}{9}\right)=0$$
|
Lời giải: $$\qquad 5\sqrt{x-1}-\sqrt{x+7}=3x-4 \quad (1)$$
Bình phương hai vế phương trình ta có: Bình phương hai vế phương trình (2) ta có: $$\Leftrightarrow (3x-4)^2(9x^2-76x+116)=0 \Leftrightarrow \left[ Thay 3 giá trị tìm được ở trên vào phương trình đã cho ta loại $x=\dfrac{58}{9}.$ Vậy phương trình có hai nghiệm $$x=\dfrac{4}{3}\quad ; \quad x=2$$.
|
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
