BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
PHẦN 6: GIẢI QUYẾT CÁC BÀI TOÁN VỀ CỰC TRỊ TRÊN TẬP SỐ PHỨC DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX
- 17/01/2019
- 1,137 lượt xem
Số phức là một chuyên đề hay và tương đối khó, thường xuất hiện trong các đề thi THPT Quốc Gia những năm gần đây. Do đó, Diễn Đàn Máy Tính Cầm Tay chúng tôi sẽ gởi đến bạn đọc chuỗi các bài viết sử dụng máy tính Casio fx 580 vnx để giải quyết nhanh các bài toán về Số Phức. Chuyên đề này bao gồm các phần:
Phần 1: Sơ lược các tính năng Số phức trên máy tính Casio fx 580 vnx
Phần 2: Giải quyết các phép toán cơ bản về số phức
Phần 3: Căn bậc hai của số phức và phương trình nghiệm phức
Phần 4: Tìm đường thẳng biểu diễn tập hợp số phức
Phần 5: Tập hợp điểm biểu diễn số phức liên quan đến đường tròn
Phần 6: Tìm cực trị trên tập số phức
Phần 7: Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc 3
Phần 8: Ứng dụng số phức vào phép tịnh tiến trong mặt phẳng
Phần 9: Ứng dụng số phức vào phép đối xứng trục và đối xứng tâm trong mặt phẳng
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]PHẦN 6: GIẢI QUYẾT CÁC BÀI TOÁN VỀ CỰC TRỊ TRÊN TẬP SỐ PHỨC DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX[/dropshadowbox]
Trong Phần 6 của Chuyên đề Số Phức, chúng tôi sẽ trình bày một số bài toán tìm GTLN và GTNN trên tập số phức bằng phương pháp tìm tập hợp điểm kết hợp với một số bất đẳng thức dưới sự hỗ trợ của Casio fx 580 vnx
Bài toán 1: (THPT chuyên Biên Hòa- Hà Nam 2017)
Cho số phức $latex z$ thỏa mãn $latex \left| z-2-4i \right|=\left| z-2i \right|$. Tìm số phức $latex z$ có môđun nhỏ nhất
- $latex z=2-2i$
- $latex z=1+i$
- $latex z=1-i$
- $latex z=2+2i$
Hướng dẫn giải:
- Tìm tập hợp điểm biểu diễn số phức $latex z$
Đặt $latex f\left( z \right)={{\left| z-2-4i \right|}^{2}}-{{\left| z-2i \right|}^{2}}$
Sử dụng Casio fx 580vnx tính $latex f\left( 0 \right)$; $latex f\left( 1 \right)$ và $latex f\left( i \right)$
- Chuyển máy tính về phương thức COMPLEX w2
- Nhập biểu thức $latex {{\left| z-2-4i \right|}^{2}}-{{\left| z-2i \right|}^{2}}$
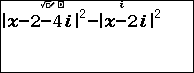
- r $x=0$
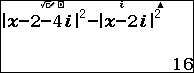
- r $latex x=1$
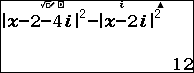
- r $latex x=i$
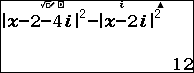
Như vậy ta có: $latex \left\{ \begin{align} & f\left( 0 \right)=16 \\ & f\left( 1 \right)=12 \\ & f\left( i \right)=12 \\\end{align} \right.$ $latex \Rightarrow \left\{ \begin{align} & c=16 \\ & a+c=12 \\ & b+c=12 \\\end{align} \right.$ $ \Rightarrow \left\{ \begin{align} & c=16 \\ & a=-4 \\ & b=-4 \\\end{align} \right.\\$
$latex \Rightarrow -4x-4y+16=0$ hay $ x+y-4=0\\$
Suy ra tập hợp số phức $latex z$ là đường thẳng $latex x+y=4$
- Tìm số phức $latex z$ thõa yêu cầu đề bài
Áp dụng bất đẳng thức Bunyakocsky ta có:
$latex \sqrt{{{1}^{2}}+{{1}^{2}}}.\sqrt{{{x}^{2}}+{{y}^{2}}}\ge x+y$ $ \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}\ge 2\sqrt{2}\\$
Dấu $latex ”=”$ xảy ra khi và chỉ khi $latex \left\{ \begin{align} & x+y=4 \\ & x=y \\\end{align} \right.$ $latex \Leftrightarrow \left\{ \begin{align} & x=2 \\ & y=2 \\\end{align} \right.$
Vậy $latex z=2+2i$
Đáp án D
Bài toán 2: Cho số phức $latex z$ thỏa mãn $latex \left| {{z}^{2}}-2z+5 \right|=\left| \left( z-1+2i \right)\left( z-1+3i \right) \right|$. Tìm giá trị nhỏ nhất của môđun số phức $latex w=z-1+i$
- $latex \dfrac{1}{2\sqrt{2}}$
- $latex \dfrac{1}{2}$
- $latex \dfrac{1}{4}$
- $latex 1$
Hướng dẫn giải
Phương trình $latex {{z}^{2}}-2z+5=0$ có nghiệm $latex {{z}_{1}}=1+2i$ và $latex {{z}_{2}}=1-2i$
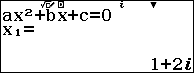
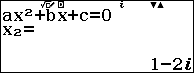
Suy ra: $ \left| {{z}^{2}}-2z+5 \right|=\left| \left( z-1+2i \right)\left( z-1+3i \right) \right|\\$
$latex \Leftrightarrow \left| \left( z-1-2i \right)\left( z-1+2i \right) \right|=\left| \left( z-1+2i \right)\left( z-1+3i \right) \right|$
$latex \Leftrightarrow \left[ \begin{align} & \left| z-1+2i \right|=0 \\ & \left| z-1-2i \right|=\left| z-1+3i \right| \\\end{align} \right.$
Trường hợp 1: $latex \left| z-1+2i \right|=0$
Khi đó: $latex \left| w+i \right|=0$ suy ra $latex \left| w \right|=1$
Trường hợp 2: $latex \left| z-1-2i \right|=\left| z-1+3i \right|$
Ta có: $latex \left| z-1-2i \right|=\left| z-1+3i \right|$$latex \Leftrightarrow {{\left| z-1-2i \right|}^{2}}-{{\left| z-1+3i \right|}^{2}}=0$
Tìm tập hợp điểm biểu diễn số phức $latex z$ thõa $latex {{\left| z-1-2i \right|}^{2}}-{{\left| z-1+3i \right|}^{2}}=0$
Đặt $latex f\left( z \right)={{\left| z-1-2i \right|}^{2}}-{{\left| z-1+3i \right|}^{2}}$
Sử dụng Casio fx 580vnx tính $latex f\left( 0 \right)$; $latex f\left( 1 \right)$ và $latex f\left( i \right)$
- Chuyển máy tính về phương thức COMPLEX w2
- Nhập biểu thức $latex {{\left| z-1-2i \right|}^{2}}-{{\left| z-1+3i \right|}^{2}}$
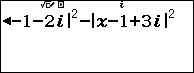
- r$x=0$
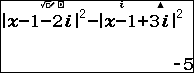
- r $latex x=1$
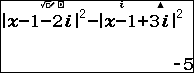
- r $latex x=i$
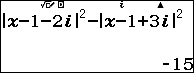
Như vậy ta có: $latex \left\{ \begin{align} & f\left( 0 \right)=-5 \\ & f\left( 1 \right)=-5 \\& f\left( i \right)=-15 \\\end{align} \right.$
$latex \Rightarrow \left\{ \begin{align} & c=-5 \\ & a+c=-5 \\ & b+c=-15 \\\end{align} \right.$ $latex \Rightarrow \left\{ \begin{align} & c=-5 \\ & a=0 \\& b=-10 \\\end{align} \right.$
$ \Rightarrow y=\dfrac{-1}{2}\\$
Suy ra: $latex w=x-1+\dfrac{i}{2}$
Khi đó: $latex {{\left| w \right|}^{2}}={{\left( x-1 \right)}^{2}}+\dfrac{1}{4}\ge \dfrac{1}{4}$
$latex \Rightarrow {{\left| w \right|}_{\min }}=\dfrac{1}{2}$ khi và chỉ khi $latex x=1$
Từ trường hợp 1 và 2 ta có $latex {{\left| w \right|}_{\min }}=\dfrac{1}{2}$
Đáp án B
Bài toán 3: Xét các số phức $latex z$ thỏa mãn $latex \left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$. Gọi $latex m,M$ lần lượt là GTNN và GTLN của $latex \left| z-1+i \right|$ . Tính $latex P=m+M$
- $latex \sqrt{13}+\sqrt{73}$
- $latex 5\sqrt{2}+\sqrt{73}$
- $latex \dfrac{5\sqrt{2}+2\sqrt{73}}{2}$
- $latex \dfrac{5\sqrt{2}+\sqrt{73}}{2}$
Hướng dẫn giải
Đặt $latex z=x+yi$
Ta có: $latex \left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$
$latex \Leftrightarrow \sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}+\sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}=6\sqrt{2}$
Theo bất đẳng thức Mincopxki ta có:
$\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}+\sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}\ge \sqrt{{{\left( x+2+4-x \right)}^{2}}+{{\left( y-1+7-y \right)}^{2}}}=6\sqrt{2}\\$
Dấu $latex ”=”$ xảy ra khi và chỉ khi $latex \left\{ \begin{align} & x+2=y-1 \\ & x-4=y-7 \\ & x\in \left[ -2;4 \right] \\ \end{align} \right.$
$latex \Leftrightarrow \left\{ \begin{align} & y=x+3 \\ & x\in \left[ -2;4 \right] \\ \end{align} \right.$
Như vậy tập hợp số phức $latex z$ thỏa điều kiện $latex \left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$ là đoạn thẳng $latex y=x+3$ với $latex x\in \left[ -2;4 \right]$
Sử dụng tính năng TABLE để tìm GTLN và GTNN của $latex \left| z-1+i \right|$
Ta có: $latex \left| z-1+i \right|=\left| x+yi-1+i \right|=\left| \left( x-1 \right)+\left( y+1 \right)i \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}}$ (thay $latex y=x+3$ )
Nhập hàm số $latex f\left( x \right)=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}}$ và $latex start=-2$; $latex end=4$ và $latex step=\dfrac{6}{29}$
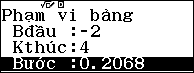
Và bảng kết quả thu được là:
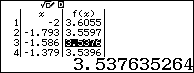
Theo bảng kết quả ta thấy
\[M=Maxf\left( x \right)=f\left( 4 \right)=\sqrt{73}\]
và ta tiếp tục kiểm tra giá trị của $latex f\left( x \right)$ với $latex x\in \left[ \dfrac{-52}{29};\dfrac{-40}{29} \right]$ để tìm giá trị xấp xỉ $latex Minf\left( x \right)$
Nhập hàm số $latex f\left( x \right)=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}}$ và $latex start=-\dfrac{52}{29}$; $latex end=\dfrac{-40}{29}$ và $latex step=\dfrac{12}{841}$
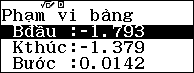
$latex m=Minf(x)\approx 3.535546003$
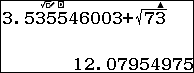
Như vậy $latex m+M\approx 12.07954975$
Đáp án: C
Cảm ơn các bạn đã theo dõi bài viết GIẢI QUYẾT CÁC BÀI TOÁN VỀ CỰC TRỊ TRÊN TẬP SỐ PHỨC DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO.
About Ngọc Hiền Bitex
